Advertisements
Advertisements
प्रश्न
A candidate is required to answer 7 questions out of 12 questions which are divided into two groups, each containing 6 questions. He is not permitted to attempt more than 5 questions from either group. In how many ways can he choose the 7 questions?
उत्तर
Required ways =
\[ = 2\left( 90 + 300 \right)\]
\[ = 2\left( 390 \right)\]
\[ = 780\]
APPEARS IN
संबंधित प्रश्न
A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected.
In an examination, a question paper consists of 12 questions divided into two parts i.e., Part I and Part II, containing 5 and 7 questions, respectively. A student is required to attempt 8 questions in all, selecting at least 3 from each part. In how many ways can a student select the questions?
It is required to seat 5 men and 4 women in a row so that the women occupy the even places. How many such arrangements are possible?
Prove that
A letter lock consists of three rings each marked with 10 different letters. In how many ways it is possible to make an unsuccessful attempt to open the lock?
How many three-digit odd numbers are there?
A number lock on a suitcase has 3 wheels each labelled with ten digits 0 to 9. If opening of the lock is a particular sequence of three digits with no repeats, how many such sequences will be possible? Also, find the number of unsuccessful attempts to open the lock.
f 24Cx = 24C2x + 3, find x.
If α = mC2, then find the value of αC2.
From a group of 15 cricket players, a team of 11 players is to be chosen. In how many ways can this be done?
How many different boat parties of 8, consisting of 5 boys and 3 girls, can be made from 25 boys and 10 girls?
From 4 officers and 8 jawans in how many ways can 6 be chosen (i) to include exactly one officer
From 4 officers and 8 jawans in how many ways can 6 be chosen. to include at least one officer?
How many triangles can be obtained by joining 12 points, five of which are collinear?
A group consists of 4 girls and 7 boys. In how many ways can a team of 5 members be selected if the team has (i) no girl?
Find the number of (i) diagonals
In how many ways can a student choose a programme of 5 courses if 9 courses are available and 2 specific courses are compulsory for every student?
If nCr + nCr + 1 = n + 1Cx , then x =
How many different committees of 5 can be formed from 6 men and 4 women on which exact 3 men and 2 women serve?
(a) 6
(b) 20
(c) 60
(d) 120
If n + 1C3 = 2 · nC2 , then n =
The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines is
Find the value of 15C4
The value of `(""^9"C"_0 + ""^9"C"_1) + (""^9"C"_1 + ""^9"C"_2) + ... + (""^9"C"_8 + ""^9"C"_9)` is ______
In how many ways can the letters of the word 'IMAGE' be arranged so that the vowels should always occupy odd places?
A student has to answer 10 questions, choosing atleast 4 from each of Parts A and B. If there are 6 questions in Part A and 7 in Part B, in how many ways can the student choose 10 questions?
We wish to select 6 persons from 8, but if the person A is chosen, then B must be chosen. In how many ways can selections be made?
A bag contains six white marbles and five red marbles. Find the number of ways in which four marbles can be drawn from the bag if they must all be of the same colour.
A group consists of 4 girls and 7 boys. In how many ways can a team of 5 members be selected if the team has at least three girls.
Total number of words formed by 2 vowels and 3 consonants taken from 4 vowels and 5 consonants is equal to ______.
Everybody in a room shakes hands with everybody else. The total number of handshakes is 66. The total number of persons in the room is ______.
Given 5 different green dyes, four different blue dyes and three different red dyes, the number of combinations of dyes which can be chosen taking at least one green and one blue dye is ______.
15C8 + 15C9 – 15C6 – 15C7 = ______.
The value of `""^50"C"_4 + sum_("r" = 1)^6 ""^(56 - "r")"C"_3` is ______.
A scientific committee is to be formed from 6 Indians and 8 foreigners, which includes at least 2 Indians and double the number of foreigners as Indians. Then the number of ways, the committee can be formed is ______.
All possible numbers are formed using the digits 1, 1, 2, 2, 2, 2, 3, 4, 4 taken all at a time. The number of such numbers in which the odd digits occupy even places is ______.
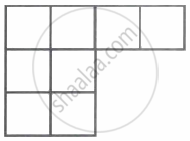
The no. of different ways, the letters of the word KUMARI can be placed in the 8 boxes of the given figure so that no row remains empty will be ______.
Total number of 6-digit numbers in which only and all the five digits 1, 3, 5, 7 and 9 appear is ______.
From 6 different novels and 3 different dictionaries, 4 novels and 1 dictionary are to be selected and arranged in a row on the shelf so that the dictionary is always in the middle. Then, the number of such arrangements is ______.
