Advertisements
Advertisements
प्रश्न
A hollow cylindrical box of length 0.5 m and area of cross-section 25 cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by `vecE = 20 xhati` where E is NC−1 and x is in metres. Find
(i) Net flux through the cylinder.
(ii) Charge enclosed by the cylinder.
उत्तर
(i) Given,
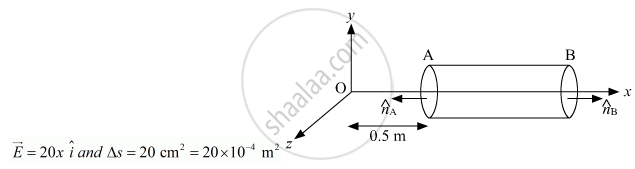
As the electric field is only along the x-axis, so, flux will pass only through the cross-section of cylinder.
Magnitude of electric field at A,
`E_A = 20 xx 0.5 = 10 N C^-1`
Magnitude of lelectic field at cross - section B
EB = 20 × 1= 20 NC-1
The corresponding eletric fluxes are
`phi_A = vecE.Δvecs = 10 xx 20 xx 10^-4 xx cos 180° = - 0.02 N m^2 C^-1`
`phi_B = vecE.Δvecs = 20 xx 20 xx 10^-4 xx cos0° = 0.04 N m^2 C^-1`
So, the net flux through the cylinder,
`phi = phi _A + phi_B = - 0.02 + 0.04 = 0.02 N m^2 C^-1 xx 10^12C`
(ii) Using Gauss’s law:
`oint vecE. vecds = q/in_0 => 0.02 = q/(8.85 xx 10^-12) => q =8.85 xx 0.02 xx 10^-12 = 0.177 xx 10^12 C`
APPEARS IN
संबंधित प्रश्न
The figure shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?

An infinite line charge produces a field of 9 × 104 N/C at a distance of 2 cm. Calculate the linear charge density.
When the separation between two charges is increased, the electric potential energy of the charges
The electric field in a region is directed outward and is proportional to the distance rfrom the origin. Taking the electric potential at the origin to be zero,
An electric field \[\vec{E} = ( \vec{i} 20 + \vec{j} 30) {NC}^{- 1}\] exists in space. If the potential at the origin is taken to be zero, find the potential at (2 m, 2 m).
The electric potential existing in space is \[\hspace{0.167em} V(x, y, z) = A(xy + yz + zx) .\] (a) Write the dimensional formula of A. (b) Find the expression for the electric field. (c) If A is 10 SI units, find the magnitude of the electric field at (1 m, 1 m, 1 m).
The kinetic energy of a charged particle decreases by 10 J as it moves from a point at potential 100 V to a point at potential 200 V. Find the charge on the particle.
The surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the center of the disc is `sigma/(2∈_0)`. With respect to the field at the center, the electric field along the axis at a distance R from the center of the disc ______.
The electric field intensity produced by the radiations coming from 100 W bulb at 3 m distance is E. The electric field intensity produced by the radiations coming from 50 W bulb at the same distance is:
