Advertisements
Advertisements
प्रश्न
A vector is not changed if
पर्याय
it is rotated through an arbitrary angle
it is multiplied by an arbitrary scalar
it is cross multiplied by a unit vector
it is slid parallel to itself.
उत्तर
it is slid parallel to itself.
A vector is defined by its magnitude and direction. If we slide it to a parallel position to itself, then none of the given parameters, which define the vector, will change.
Let the magnitude of a displacement vector ( \[\vec{A}\] ) directed towards the north be 5 metres. If we slide it parallel to itself, then the direction and magnitude will not change.
APPEARS IN
संबंधित प्रश्न
What are the dimensions of volume of a sphere of radius a?
A physical quantity is measured and the result is expressed as nu where u is the unit used and n is the numerical value. If the result is expressed in various units then
The dimensions ML−1 T−2 may correspond to
Find the dimensions of the specific heat capacity c.
(a) the specific heat capacity c,
(b) the coefficient of linear expansion α and
(c) the gas constant R.
Some of the equations involving these quantities are \[Q = mc\left( T_2 - T_1 \right), l_t = l_0 \left[ 1 + \alpha\left( T_2 - T_1 \right) \right]\] and PV = nRT.
Test if the following equation is dimensionally correct:
\[v = \sqrt{\frac{P}{\rho}},\]
where v = velocity, ρ = density, P = pressure
Test if the following equation is dimensionally correct:
\[V = \frac{\pi P r^4 t}{8 \eta l}\]
where v = frequency, P = pressure, η = coefficient of viscosity.
Test if the following equation is dimensionally correct:
\[v = \frac{1}{2 \pi}\sqrt{\frac{mgl}{I}};\]
where h = height, S = surface tension, \[\rho\] = density, P = pressure, V = volume, \[\eta =\] coefficient of viscosity, v = frequency and I = moment of interia.
Is it possible to add two vectors of unequal magnitudes and get zero? Is it possible to add three vectors of equal magnitudes and get zero?
Let ε1 and ε2 be the angles made by \[\vec{A}\] and -\[\vec{A}\] with the positive X-axis. Show that tan ε1 = tan ε2. Thus, giving tan ε does not uniquely determine the direction of \[\vec{A}\].
Can you have \[\vec{A} \times \vec{B} = \vec{A} \cdot \vec{B}\] with A ≠ 0 and B ≠ 0 ? What if one of the two vectors is zero?
The radius of a circle is stated as 2.12 cm. Its area should be written as
The x-component of the resultant of several vectors
(a) is equal to the sum of the x-components of the vectors of the vectors
(b) may be smaller than the sum of the magnitudes of the vectors
(c) may be greater than the sum of the magnitudes of the vectors
(d) may be equal to the sum of the magnitudes of the vectors.
Let \[\vec{A} \text { and } \vec{B}\] be the two vectors of magnitude 10 unit each. If they are inclined to the X-axis at angle 30° and 60° respectively, find the resultant.
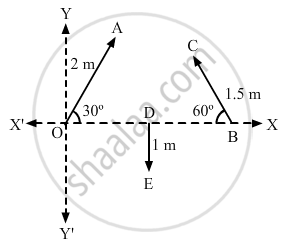
Refer to figure (2 − E1). Find (a) the magnitude, (b) x and y component and (c) the angle with the X-axis of the resultant of \[\overrightarrow{OA}, \overrightarrow{BC} \text { and } \overrightarrow{DE}\].
Suppose \[\vec{a}\] is a vector of magnitude 4.5 units due north. What is the vector (a) \[3 \vec{a}\], (b) \[- 4 \vec{a}\] ?
If \[\vec{A} , \vec{B} , \vec{C}\] are mutually perpendicular, show that \[\vec{C} \times \left( \vec{A} \times \vec{B} \right) = 0\] Is the converse true?
Give an example for which \[\vec{A} \cdot \vec{B} = \vec{C} \cdot \vec{B} \text{ but } \vec{A} \neq \vec{C}\].
A curve is represented by y = sin x. If x is changed from \[\frac{\pi}{3}\text{ to }\frac{\pi}{3} + \frac{\pi}{100}\] , find approximately the change in y.
The changes in a function y and the independent variable x are related as
\[\frac{dy}{dx} = x^2\] . Find y as a function of x.
Write the number of significant digits in (a) 1001, (b) 100.1, (c) 100.10, (d) 0.001001.
