Advertisements
Advertisements
प्रश्न
Let ε1 and ε2 be the angles made by \[\vec{A}\] and -\[\vec{A}\] with the positive X-axis. Show that tan ε1 = tan ε2. Thus, giving tan ε does not uniquely determine the direction of \[\vec{A}\].
उत्तर
The direction of - \[\vec{A}\] is opposite to \[\vec{A}\].So, if vector \[\vec{A}\] and \[- \vec{A}\] make the angles ε1 and ε2 with the X-axis, respectively, then ε1 is equal to ε2 as shown in the figure:
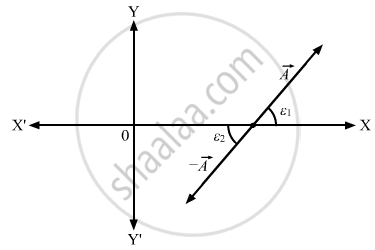
Here, tan ε1 = tan ε2
Because these are alternate angles.
Thus, giving tan ε does not uniquely determine the direction of \[- \vec{A}\].
APPEARS IN
संबंधित प्रश्न
“Politics is the art of the possible”. Similarly, “Science is the art of the soluble”. Explain this beautiful aphorism on the nature and practice of science.
What are the dimensions of volume of a sphere of radius a?
If two quantities have same dimensions, do they represent same physical content?
\[\int\frac{dx}{\sqrt{2ax - x^2}} = a^n \sin^{- 1} \left[ \frac{x}{a} - 1 \right]\]
The value of n is
Find the dimensions of pressure.
Find the dimensions of the coefficient of linear expansion α and
The height of mercury column in a barometer in a Calcutta laboratory was recorded to be 75 cm. Calculate this pressure in SI and CGS units using the following data : Specific gravity of mercury = \[13 \cdot 6\] , Density of \[\text{ water} = {10}^3 kg/ m^3 , g = 9 \cdot 8 m/ s^2\] at Calcutta. Pressure
= hpg in usual symbols.
Let x and a stand for distance. Is
\[\int\frac{dx}{\sqrt{a^2 - x^2}} = \frac{1}{a} \sin^{- 1} \frac{a}{x}\] dimensionally correct?
Is it possible to add two vectors of unequal magnitudes and get zero? Is it possible to add three vectors of equal magnitudes and get zero?
If \[\vec{A} \times \vec{B} = 0\] can you say that
(a) \[\vec{A} = \vec{B} ,\]
(b) \[\vec{A} \neq \vec{B}\] ?
The component of a vector is
The radius of a circle is stated as 2.12 cm. Its area should be written as
Let \[\vec{C} = \vec{A} + \vec{B}\]
The magnitude of the vector product of two vectors \[\left| \vec{A} \right|\] and \[\left| \vec{B} \right|\] may be
(a) greater than AB
(b) equal to AB
(c) less than AB
(d) equal to zero.
A vector \[\vec{A}\] makes an angle of 20° and \[\vec{B}\] makes an angle of 110° with the X-axis. The magnitudes of these vectors are 3 m and 4 m respectively. Find the resultant.
Two vectors have magnitudes 2 m and 3m. The angle between them is 60°. Find (a) the scalar product of the two vectors, (b) the magnitude of their vector product.
Prove that \[\vec{A} . \left( \vec{A} \times \vec{B} \right) = 0\].
Give an example for which \[\vec{A} \cdot \vec{B} = \vec{C} \cdot \vec{B} \text{ but } \vec{A} \neq \vec{C}\].
A curve is represented by y = sin x. If x is changed from \[\frac{\pi}{3}\text{ to }\frac{\pi}{3} + \frac{\pi}{100}\] , find approximately the change in y.
