Advertisements
Advertisements
Question
Let ε1 and ε2 be the angles made by \[\vec{A}\] and -\[\vec{A}\] with the positive X-axis. Show that tan ε1 = tan ε2. Thus, giving tan ε does not uniquely determine the direction of \[\vec{A}\].
Solution
The direction of - \[\vec{A}\] is opposite to \[\vec{A}\].So, if vector \[\vec{A}\] and \[- \vec{A}\] make the angles ε1 and ε2 with the X-axis, respectively, then ε1 is equal to ε2 as shown in the figure:
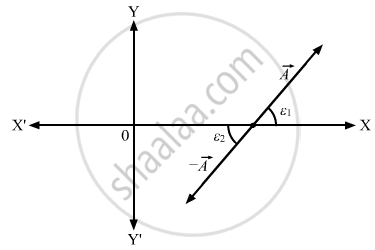
Here, tan ε1 = tan ε2
Because these are alternate angles.
Thus, giving tan ε does not uniquely determine the direction of \[- \vec{A}\].
APPEARS IN
RELATED QUESTIONS
“Every great physical theory starts as a heresy and ends as a dogma”. Give some examples from the history of science of the validity of this incisive remark
India has had a long and unbroken tradition of great scholarship — in mathematics, astronomy, linguistics, logic and ethics. Yet, in parallel with this, several superstitious and obscurantistic attitudes and practices flourished in our society and unfortunately continue even today — among many educated people too. How will you use your knowledge of science to develop strategies to counter these attitudes ?
What are the dimensions of volume of a sphere of radius a?
Suggest a way to measure the thickness of a sheet of paper.
A physical quantity is measured and the result is expressed as nu where u is the unit used and n is the numerical value. If the result is expressed in various units then
Suppose a quantity x can be dimensionally represented in terms of M, L and T, that is, `[ x ] = M^a L^b T^c`. The quantity mass
A unitless quantity
Find the dimensions of electric field E.
The relevant equations are \[F = qE, F = qvB, \text{ and }B = \frac{\mu_0 I}{2 \pi a};\]
where F is force, q is charge, v is speed, I is current, and a is distance.
Find the dimensions of magnetic permeability \[\mu_0\]
The relevant equation are \[F = qE, F = qvB, \text{ and }B = \frac{\mu_0 I}{2 \pi a};\]
where F is force, q is charge, v is speed, I is current, and a is distance.
Test if the following equation is dimensionally correct:
\[V = \frac{\pi P r^4 t}{8 \eta l}\]
where v = frequency, P = pressure, η = coefficient of viscosity.
Let x and a stand for distance. Is
\[\int\frac{dx}{\sqrt{a^2 - x^2}} = \frac{1}{a} \sin^{- 1} \frac{a}{x}\] dimensionally correct?
Is a vector necessarily changed if it is rotated through an angle?
Can a vector have zero component along a line and still have nonzero magnitude?
Let \[\vec{A} = 3 \vec{i} + 4 \vec{j}\]. Write a vector \[\vec{B}\] such that \[\vec{A} \neq \vec{B}\], but A = B.
The resultant of \[\vec{A} \text { and } \vec{B}\] makes an angle α with \[\vec{A}\] and β with \[\vec{B}\],
Let the angle between two nonzero vectors \[\vec{A}\] and \[\vec{B}\] be 120° and its resultant be \[\vec{C}\].
The x-component of the resultant of several vectors
(a) is equal to the sum of the x-components of the vectors of the vectors
(b) may be smaller than the sum of the magnitudes of the vectors
(c) may be greater than the sum of the magnitudes of the vectors
(d) may be equal to the sum of the magnitudes of the vectors.
Two vectors have magnitudes 2 m and 3m. The angle between them is 60°. Find (a) the scalar product of the two vectors, (b) the magnitude of their vector product.
Draw a graph from the following data. Draw tangents at x = 2, 4, 6 and 8. Find the slopes of these tangents. Verify that the curve draw is y = 2x2 and the slope of tangent is \[\tan \theta = \frac{dy}{dx} = 4x\]
\[\begin{array}x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ y & 2 & 8 & 18 & 32 & 50 & 72 & 98 & 128 & 162 & 200\end{array}\]
Write the number of significant digits in (a) 1001, (b) 100.1, (c) 100.10, (d) 0.001001.
