Advertisements
Advertisements
प्रश्न
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/h more than that of the passenger train, find the average speed of the two trains.
उत्तर
Let the speed of the passenger train be x km/hr.
Speed of the express train = (x + 11) km/hr
Time taken by the passenger train to cover 132 km between Mysore to Bangalore `132/x` hr
Time taken by the express train to cover 132 km between Mysore to Bangalore = `132/(x+11)` hr
Therefore,
`132/x - 132/(x + 11)` = 1
`(132(x + 11) - 132x)/(x(x + 11))` = 1
`(132x + 1452 - 132x)/(x^2 + 11)`= 1
`1452/(x^2 + 11)` = 1
1452 = x2 + 11
x2 + 11 – 1452 = 0
x2 – 33x + 44x – 1452 = 0
x(x – 33) + 44(x – 33) = 0
(x – 33)(x + 44) = 0
So, either
x – 33 = 0
x = 33
Or
x + 44 = 0
x = – 44
But, the speed of the train can never be negative.
Thus, when x = 33 then the speed of the express train
= x + 11
= 33 + 11
= 44
Hence, the speed of the passenger train is x = 33 km/hr
and the speed of the express train is x = 44 km/hr respectively.
APPEARS IN
संबंधित प्रश्न
Solve the following quadratic equation for x: `4x^2 + 4bx – (a^2 – b^2) = 0`
Find the roots of the quadratic equation 4x2 + 4√3x + 3 = 0
Find the root of the following equation.
`1/(x+4) - 1/(x-7) = 11/30, x ≠ -4, 7`
Sum of the areas of two squares is 468 m2. If the difference of their perimeters is 24 m, find the sides of the two squares.
Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
`sqrt3x^2+10x+7sqrt3=0`
`3x^2-2x-1=0`
`2/x^2-5/x+2=0`
`sqrt3x^2+10x+7sqrt3=0`
The length of a rectangle is thrice as long as the side of a square. The side of the square is 4 cm more than the width of the rectangle. Their areas being equal, find the dimensions.
The area of right-angled triangle is 96 sq meters. If the base is three time the altitude, find the base.
The hypotenuse of a right=-angled triangle is 20 meters. If the difference between the lengths of the other sides be 4 meters, find the other sides
Solve the following quadratic equation by completing the square method.
x2 + 2x – 5 = 0
Solve the following quadratic equation by completing the square method.
5x2 = 4x + 7
Fill in the gaps and complete.
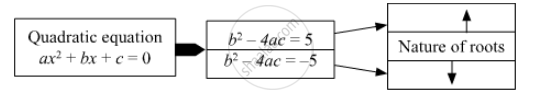
Find the value of discriminant.
x2 + 7x – 1 = 0
Form the quadratic equation from the roots given below.
3 and –10
α, β are roots of y2 – 2y –7 = 0 find,
α2 + β2
α, β are roots of y2 – 2y –7 = 0 find,
α3 + β3
The sum of the squares of two consecutive multiples of 7 is 637. Find the multiples.
The numerator of a fraction is 3 less than the denominator. If 2 is added to both the numerator and the denominator, then the sum of the new fraction and the original fraction is \[\frac{29}{20}\].Find the original fraction.
The value of \[\sqrt{6 + \sqrt{6 + \sqrt{6 +}}} . . . .\] is
A chess board contains 64 equal squares and the area of each square is 6.25 cm2. A border round the board is 2 cm wide. The length of the side of the chess board is:
The value of `sqrt(6 + sqrt(6 + sqrt(6 ....)))`
The positive root of `sqrt(3"x"^2 + 6)` = 9 is:
If Ritu were younger by 5 years than what she really is, then the square of her age would have been 11 more than five times her present age. What is her present age?
Find the remainder when p(x) = 3x2 + 2x – 7 is divided by 2x + 1.
Find the value of x, if `(4/7)^x (7/4)^(2x) = 343/64`.
Find the value of x, if `5^(x - 3) xx 5^(2x – 8)` = 625.
