Advertisements
Advertisements
प्रश्न
Answer the following question:
The vertices of a triangle are A(1, 4), B(2, 3) and C(1, 6). Find equations of the medians.
उत्तर
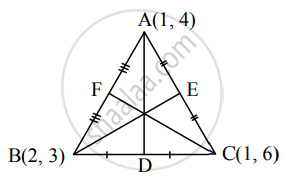
Let D, E, and F be the midpoints of sides BC, AC, and AB respectively of ΔABC.
Then D ≡ `((2 + 1)/2, (3 + 6)/2) = (3/2, 9/2)`
E ≡ `((1 + 1)/2, (6 + 4)/2)` = (1, 5)
F ≡ `((1 + 2)/2, (4 + 3)/2) = (3/2, 7/2)`
Equation of median AD is
`(y - 4)/(9/2 - 4) = (x - 1)/(3/2 - 1)`
∴ `(y - 4)/(1/2) = (x - 1)/(1/2)`
∴ x – y + 3 = 0
Equation of median BE is
`(y - 3)/(5 - 3) = (x - 2)/(1 - 2)`
∴ – 1(y – 3) = 2(x – 2)
∴ – y + 3 = 2x – 4
∴ 2x + y = 7
Equation of median CF is
`(y - 6)/(7/2 - 6) = (x - 1)/(3/2 - 1)`
∴ `(y - 6)/(-5/2) = (x - 1)/(1/2)`
∴ y – 6 = – 5(x – 1)
∴ 5x + y – 11 = 0
APPEARS IN
संबंधित प्रश्न
Write the equation of the line :
parallel to the X−axis and at a distance of 5 unit form it and above it
Write the equation of the line :
parallel to the Y−axis and at a distance of 5 unit form it and to the left of it
Obtain the equation of the line containing the point :
A(2, – 3) and parallel to the Y−axis
Obtain the equation of the line containing the point :
B(4, –3) and parallel to the X-axis
Find the equation of the line passing through the points A(2, 0), and B(3, 4)
Find the equation of the line passing through the origin and which bisects the portion of the line 3x + y = 6 intercepted between the co-ordinate axes.
Find the equation of the line having inclination 135° and making X-intercept 7
The vertices of a triangle are A(3, 4), B(2, 0), and C(−1, 6). Find the equation of the line containing side BC.
The vertices of a triangle are A(3, 4), B(2, 0), and C(−1, 6). Find the equation of the line containing the median AD
Find the x and y intercept of the following line:
2x − 3y + 12 = 0
Find equations of lines containing the point A(3, 4) and making equal intercepts on the co-ordinates axes.
Select the correct option from the given alternatives:
If the line kx + 4y = 6 passes through the point of intersection of the two lines 2x + 3y = 4 and 3x + 4y = 5, then k =
Answer the following question:
Does point A(2, 3) lie on the line 3x + 2y – 6 = 0? Give reason.
Answer the following question:
Find the equation of the line passing through the points S(2, 1) and T(2, 3)
Answer the following question:
The vertices of a triangle are A(1, 4), B(2, 3) and C(1, 6). Find equations of the sides.
Answer the following question:
The vertices of a triangle are A(1, 4), B(2, 3) and C(1, 6) Find equations of Perpendicular bisectors of sides
Answer the following question:
Find the X−intercept of the line whose slope is 3 and which makes intercept 4 on the Y−axis
Answer the following question:
Find the equations of the diagonals of the rectangle whose sides are contained in the lines x = 8, x = 10, y = 11 and y = 12
Answer the following question:
A(1, 4), B(2, 3) and C(1, 6) are vertices of ∆ABC. Find the equation of the altitude through B and hence find the co-ordinates of the point where this altitude cuts the side AC of ∆ABC.
Answer the following question:
The vertices of ∆PQR are P(2, 1), Q(−2, 3) and R(4, 5). Find the equation of the median through R.
Answer the following question:
A line perpendicular to segment joining A(1, 0) and B(2, 3) divides it internally in the ratio 1 : 2. Find the equation of the line.
Answer the following question:
Find the co-ordinates of the foot of the perpendicular drawn from the point P(−1, 3) the line 3x − 4y − 16 = 0
Answer the following question:
The perpendicular from the origin to a line meets it at (−2, 9). Find the equation of the line.
Answer the following question:
Show that there are two lines which pass through A(3, 4) and the sum of whose intercepts is zero.
Answer the following question:
Show that there is only one line which passes through B(5, 5) and the sum of whose intercept is zero.
If the equation kxy + 5x + 3y + 2 = 0 represents a pair of lines, then k = ____________.
If (a, −2a), a > 0 is the mid-point of a line segment intercepted between the co-ordinate axes, then the equation of the line is ____________.
The lines `(x + 1)/(-10) = (y + 3)/-1 = (z - 4)/1` and `(x + 10)/(-1) = (y + 1)/-3 = (z - 1)/4` intersect at the point ______
The line L given by `x/5+y/b=1` passes through the point (13, 32). The line K is parallel to L and its equation is `x/c+y/3=1`. Then, the distance between L and K is ______.
The angle between the lines x sin 60° + y cos 60° = 5 and x sin 30° + y cos 30° = 7 is ______
Let the perpendiculars from any point on the line 7x + 56y = 0 upon 3x + 4y = 0 and 5x – 12y = 0 be p and p', then ______.
Area of the parallelogram formed by the lines y = mx, y = mx + 1, y = nx and y = nx + 1 is equal to ______.
N(3, – 4) is the foot of the perpendicular drawn from the origin to a line L. Then, the equation of the line L is ______.
