Advertisements
Advertisements
प्रश्न
Answer the following question:
The vertices of a triangle are A(1, 4), B(2, 3) and C(1, 6). Find equations of the medians.
उत्तर
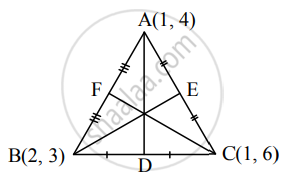
Let D, E, and F be the midpoints of sides BC, AC, and AB respectively of ΔABC.
Then D ≡ `((2 + 1)/2, (3 + 6)/2) = (3/2, 9/2)`
E ≡ `((1 + 1)/2, (6 + 4)/2)` = (1, 5)
F ≡ `((1 + 2)/2, (4 + 3)/2) = (3/2, 7/2)`
Equation of median AD is
`(y - 4)/(9/2 - 4) = (x - 1)/(3/2 - 1)`
∴ `(y - 4)/(1/2) = (x - 1)/(1/2)`
∴ x – y + 3 = 0
Equation of median BE is
`(y - 3)/(5 - 3) = (x - 2)/(1 - 2)`
∴ – 1(y – 3) = 2(x – 2)
∴ – y + 3 = 2x – 4
∴ 2x + y = 7
Equation of median CF is
`(y - 6)/(7/2 - 6) = (x - 1)/(3/2 - 1)`
∴ `(y - 6)/(-5/2) = (x - 1)/(1/2)`
∴ y – 6 = – 5(x – 1)
∴ 5x + y – 11 = 0
APPEARS IN
संबंधित प्रश्न
Write the equation of the line :
parallel to the X-axis and at a distance of 4 unit form the point (−2, 3)
Obtain the equation of the line :
parallel to the Y−axis and making an intercept of 4 unit on the X−axis
Obtain the equation of the line containing the point :
A(2, – 3) and parallel to the Y−axis
Find the equation of the line passing through the points A(2, 0), and B(3, 4)
Find the equation of the line having slope `1/2` and containing the point (3, −2).
Find the equation of the line containing point A(3, 5) and having slope `2/3`.
Find the equation of the line passing through the origin and which bisects the portion of the line 3x + y = 6 intercepted between the co-ordinate axes.
The vertices of a triangle are A(3, 4), B(2, 0), and C(−1, 6). Find the equation of the line containing the midpoints of sides AB and BC
Find the x and y intercept of the following line:
2x − 3y + 12 = 0
Find the equations of perpendicular bisectors of sides of the triangle whose vertices are P(−1, 8), Q(4, −2), and R(−5, −3)
N(3, −4) is the foot of the perpendicular drawn from the origin to line L. Find the equation of line L.
Answer the following question:
Reduce the equation 6x + 3y + 8 = 0 into slope-intercept form. Hence find its slope
Answer the following question:
Does point A(2, 3) lie on the line 3x + 2y – 6 = 0? Give reason.
Answer the following question:
Obtain the equation of the line containing the point (2, 3) and parallel to the X-axis.
Answer the following question:
Find the equation of the line through the origin which bisects the portion of the line 3x + 2y = 2 intercepted between the co−ordinate axes.
Answer the following question:
Find the equation of the line which contains the point A(3, 5) and makes equal intercepts on the co-ordinates axes.
Answer the following question:
The vertices of a triangle are A(1, 4), B(2, 3) and C(1, 6). Find equations of the sides.
Answer the following question:
The vertices of a triangle are A(1, 4), B(2, 3) and C(1, 6) Find equations of altitudes of ∆ABC
Answer the following question:
Two lines passing through M(2, 3) intersect each other at an angle of 45°. If slope of one line is 2, find the equation of the other line.
Answer the following question:
Find the equations of the diagonals of the rectangle whose sides are contained in the lines x = 8, x = 10, y = 11 and y = 12
Answer the following question:
The perpendicular from the origin to a line meets it at (−2, 9). Find the equation of the line.
If (a, −2a), a > 0 is the mid-point of a line segment intercepted between the co-ordinate axes, then the equation of the line is ____________.
The lines `(x + 1)/(-10) = (y + 3)/-1 = (z - 4)/1` and `(x + 10)/(-1) = (y + 1)/-3 = (z - 1)/4` intersect at the point ______
The slope of normal to the curve x = `sqrt"t"` and y = `"t" - 1/sqrt"t"`at t = 4 is _____.
The point A(b, a) lies on the straight line 2x + 3y = 13 and the point B(a, b) lies on the straight line -x + 4y = 5, then the equation of line AB is ______
The intercept of a line between the coordinate axes is divided by the point (1, 3) in the ratio 3 : 1. The equation of the line will be ______
The line L given by `x/5+y/b=1` passes through the point (13, 32). The line K is parallel to L and its equation is `x/c+y/3=1`. Then, the distance between L and K is ______.
Suppose the line `(x - 2)/α = ("y" - 2)/(-5) = ("z" + 2)/2` lies on the plane x + 3y – 2z + β = 0. Then (α + β) is equal to ______.
Area of the parallelogram formed by the lines y = mx, y = mx + 1, y = nx and y = nx + 1 is equal to ______.
N(3, – 4) is the foot of the perpendicular drawn from the origin to a line L. Then, the equation of the line L is ______.
