Advertisements
Advertisements
प्रश्न
Consider the situation of the previous problem. Consider the faster electron emitted parallel to the large metal plate. Find the displacement of this electron parallel to its initial velocity before it strikes the large metal plate.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
उत्तर
Electric field of the metal plate,
`E = σ/∈_0 = (1 xx 10^-9)/(8.85 xx 10^-12)`
= 113 V/m
Acceleration,
`a = (qE)/m`,
where q=charge on electron
E=electric field
m=mass of electron
`a = (1.6 xx 10^-19 xx 113)/(9.1 xx 10^-31) = 19.87 xx 10^12`
`t = sqrt((2y)/a) = sqrt((2 xx 20 xx 10^-2)/(19.87 xx 10^12)`
=`1.41 xx 10^-7` s
From Einstein's photoelectric equation,
`K.E. = (hc)/lambda - W = 1.2 "eV"`
= `1.2 xx 1.6 xx 10^-19 "J"...........[because "in problem " 31 : "KE" = 1.2 "eV"`]
`therefore "Velocity", v = sqrt({2KE)/m)`
`= sqrt((2 xx 1.2 xx 1.6 xx 10^-19)/(4.1 xx 10^-31))` `sqrt((2 xx 1.2 xx 1.6 xx 10^-19)/(4.1 xx 10^-31))`
`= 0.665 xx 10^-6 "m/s"`
∴ Horizontal displacement,
`S = v xx t`
`S = 0.665 xx 10^-6 xx 1.4 xx 10^-7`
`S = 0.092 "m" = 9.2 "cm"`
APPEARS IN
संबंधित प्रश्न
In an experiment on the photoelectric effect, the slope of the cut-off voltage versus the frequency of incident light is found to be 4.12 × 10−15 Vs. Calculate the value of Planck’s constant.
Plot a graph showing the variation of photoelectric current with collector plate potential at a given frequency but for two different intensities I1 and I2, where I2 > I1.
A non-monochromatic light is used in an experiment on photoelectric effect. The stopping potential
A monochromatic light source of intensity 5 mW emits 8 × 1015 photons per second. This light ejects photoelectrons from a metal surface. The stopping potential for this setup is 2.0 V. Calculate the work function of the metal.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
A small metal plate (work function φ) is kept at a distance d from a singly-ionised, fixed ion. A monochromatic light beam is incident on the metal plate and photoelectrons are emitted. Find the maximum wavelength of the light beam, so that some of the photoelectrons may go round the ion along a circle.
In a photoelectric experiment, the collector plate is at 2.0 V with respect to the emitter plate made of copper (φ = 4.5 eV). The emitter is illuminated by a source of monochromatic light of wavelength 200 nm. Find the minimum and maximum kinetic energy of the photoelectrons reaching the collector.
Use Einstein’s photoelectric equation to show how from this graph,
(i) Threshold frequency, and (ii) Planck’s constant can be determined.
How does one explain the emission of electrons from a photosensitive surface with the help of Einstein’s photoelectric equation?
Use Einstein's photoelectric equation to show how from this graph,
(i) Threshold frequency, and
(ii) Planck's constant can be determined.
Choose the correct answer from given options
Photons of frequency v are incident on the surface of two metals A and B of threshold frequency 3/4 v and 2/3 v, respectively. The ratio of maximum kinetic energy of electrons emitted from A to that from B is
According to Einstein's photoelectric equation, the plot of the kinetic energy of the emitted photoelectrons from a metal versus the frequency of the incident radiation gives a straight line, whose slope ______.
The minimum energy required to remove an electron is called ______.
A student performs an experiment on photoelectric effect, using two materials A and B. A plot of Vstop vs ν is given in Figure.
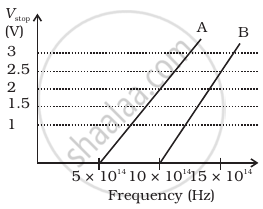
- Which material A or B has a higher work function?
- Given the electric charge of an electron = 1.6 × 10–19 C, find the value of h obtained from the experiment for both A and B.
Comment on whether it is consistent with Einstein’s theory:
A photon of wavelength 663 nm is incident on a metal surface. The work function of the metal is 1.50 eV. The maximum kinetic energy of the emitted photoelectrons is ______.
The photon emitted during the de-excitation from the first excited level to the ground state of a hydrogen atom is used to irradiate a photocathode in which the stopping potential is 5 V. Calculate the work function of the cathode used.
