Advertisements
Advertisements
प्रश्न
उत्तर
We have,
\[\frac{dy}{dx} + 2y = x e^{4x} . . . . . \left( 1 \right)\]
Clearly, it is a linear differential equation of the form
\[\frac{dy}{dx} + Py = Q\]
where
\[P = 2\]
\[Q = x e^{4x} \]
\[ \therefore I.F. = e^{\int P\ dx} \]
\[ = e^{ \int2dx } \]
\[ = e^{2x} \]
\[\text{Multiplying both sides of }\left( 1 \right)\text{ by }e^{2x} ,\text{ we get }\]
\[ e^{2x} \left( \frac{dy}{dx} + 2y \right) = e^{2x} \times x e^{4x} \]
\[ \Rightarrow e^{2x} \frac{dy}{dx} + 2 e^{2x} y = x e^{6x} \]
Integrating both sides with respect to x, we get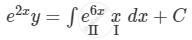
\[ \Rightarrow e^{2x} y = x\int e^{6x} dx - \int\left[ \frac{d}{dx}\left( x \right)\int e^{6x} dx \right]dx + C\]
\[ \Rightarrow e^{2x} y = \frac{x e^{6x}}{6} - \frac{e^{6x}}{36} + C\]
\[ \Rightarrow y = \frac{x e^{4x}}{6} - \frac{e^{4x}}{36} + C e^{- 2x} \]
\[\text{ Hence, }y = \frac{x e^{4x}}{6} - \frac{e^{4x}}{36} + C e^{- 2x}\text{ is the required solution.}\]
APPEARS IN
संबंधित प्रश्न
For the differential equation, find the general solution:
`dy/dx + y/x = x^2`
For the differential equation, find the general solution:
`dy/dx + (sec x) y = tan x (0 <= x < pi/2)`
For the differential equation, find the general solution:
`cos^2 x dy/dx + y = tan x(0 <= x < pi/2)`
The population of a village increases continuously at the rate proportional to the number of its inhabitants present at any time. If the population of the village was 20000 in 1999 and 25000 in the year 2004, what will be the population of the village in 2009?
x dy = (2y + 2x4 + x2) dx
\[\frac{dy}{dx}\] = y tan x − 2 sin x
Solve the differential equation \[\left( x + 2 y^2 \right)\frac{dy}{dx} = y\], given that when x = 2, y = 1.
Find the general solution of the differential equation \[\frac{dy}{dx} - y = \cos x\]
Solve the differential equation \[\left( y + 3 x^2 \right)\frac{dx}{dy} = x\]
Solve the following differential equation: \[\left( \cot^{- 1} y + x \right) dy = \left( 1 + y^2 \right) dx\] .
Find the integerating factor of the differential equation `xdy/dx - 2y = 2x^2` .
If f(x) = x + 1, find `"d"/"dx"("fof") ("x")`
Solve the differential equation: `(1 + x^2) dy/dx + 2xy - 4x^2 = 0,` subject to the initial condition y(0) = 0.
Solve the following differential equation:
`"dy"/"dx" + "y"/"x" = "x"^3 - 3`
Solve the following differential equation:
`("x + y") "dy"/"dx" = 1`
Solve the following differential equation:
`(1 - "x"^2) "dy"/"dx" + "2xy" = "x"(1 - "x"^2)^(1/2)`
Find the equation of the curve which passes through the origin and has the slope x + 3y - 1 at any point (x, y) on it.
Find the equation of the curve passing through the point `(3/sqrt2, sqrt2)` having a slope of the tangent to the curve at any point (x, y) is -`"4x"/"9y"`.
Form the differential equation of all circles which pass through the origin and whose centers lie on X-axis.
The integrating factor of the differential equation (1 + x2)dt = (tan-1 x - t)dx is ______.
The slope of the tangent to the curves x = 4t3 + 5, y = t2 - 3 at t = 1 is ______
Which of the following is a second order differential equation?
Integrating factor of the differential equation `(1 - x^2) ("d"y)/("d"x) - xy` = 1 is ______.
The equation x2 + yx2 + x + y = 0 represents
The integrating factor of the differential equation `x (dy)/(dx) - y = 2x^2` is
The integrating factor of differential equation `(1 - y)^2 (dx)/(dy) + yx = ay(-1 < y < 1)`
If y = y(x) is the solution of the differential equation, `(dy)/(dx) + 2ytanx = sinx, y(π/3)` = 0, then the maximum value of the function y (x) over R is equal to ______.
If the slope of the tangent at (x, y) to a curve passing through `(1, π/4)` is given by `y/x - cos^2(y/x)`, then the equation of the curve is ______.
The solution of the differential equation `dx/dt = (xlogx)/t` is ______.
If sec x + tan x is the integrating factor of `dy/dx + Py` = Q, then value of P is ______.
The slope of the tangent to the curve x = sin θ and y = cos 2θ at θ = `π/6` is ______.
