Advertisements
Advertisements
प्रश्न
उत्तर
We have,
\[\frac{dy}{dx} + y \tan x = x^2 \cos^2 x\]
\[P = \tan x \]
\[Q = x^2 \cos^2 x\]
Now,
\[I . F . = e^{\int\tan x\ dx} = e^{log \left| \sec x \right|} = \sec x\]
Therefore, solution is given by
\[y \times I . F . = \int x^2 \cos^2 x \times I . F . dx + C\]
\[ \Rightarrow y \sec x = \int x^2 \cos x dx + C\]
\[ \Rightarrow y \sec x = I + C\]
Where,
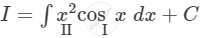
\[ \Rightarrow I = x^2 \sin x - 2\int x \sin x dx\]
\[ \Rightarrow I = x^2 \sin x - 2\int x_I \sin x_{II} dx\]
\[ \Rightarrow I = x^2 \sin x - 2x\int\sin x dx + 2\int\left[ \frac{d}{dx}\left( x \right)\int\sin x dx \right]dx\]
\[ \Rightarrow I = x^2 \sin x + 2x \cos x - 2\int\cos x dx\]
\[ \Rightarrow I = x^2 \sin x + 2x \cos x - 2\sin x\]
\[ \Rightarrow I = x^2 \sin x + 2x \cos x - 2\sin x\]
\[ \therefore y \sec x = x^2 \sin x + 2x \cos x - 2\sin x + C\]
\[ \Rightarrow y \sec x = x^2 \sin x + 2x \cos x - 2\sin x + C\]
APPEARS IN
संबंधित प्रश्न
For the differential equation given, find a particular solution satisfying the given condition:
`(1 + x^2)dy/dx + 2xy = 1/(1 + x^2); y = 0` when x = 1
Find the equation of a curve passing through the point (0, 2) given that the sum of the coordinates of any point on the curve exceeds the magnitude of the slope of the tangent to the curve at that point by 5.
The population of a village increases continuously at the rate proportional to the number of its inhabitants present at any time. If the population of the village was 20000 in 1999 and 25000 in the year 2004, what will be the population of the village in 2009?
Find the general solution of the differential equation `dy/dx - y = sin x`
Solve the differential equation `x dy/dx + y = x cos x + sin x`, given that y = 1 when `x = pi/2`
dx + xdy = e−y sec2 y dy
Find the general solution of the differential equation \[x\frac{dy}{dx} + 2y = x^2\]
Solve the differential equation \[\left( y + 3 x^2 \right)\frac{dx}{dy} = x\]
Solve the following differential equation: \[\left( \cot^{- 1} y + x \right) dy = \left( 1 + y^2 \right) dx\] .
Solve the differential equation \[\frac{dy}{dx}\] + y cot x = 2 cos x, given that y = 0 when x = \[\frac{\pi}{2}\] .
Find the integerating factor of the differential equation `xdy/dx - 2y = 2x^2` .
Solve the differential equation: `(1 + x^2) dy/dx + 2xy - 4x^2 = 0,` subject to the initial condition y(0) = 0.
Solve the following differential equation:
`"dy"/"dx" + "y"/"x" = "x"^3 - 3`
Solve the following differential equation:
`cos^2 "x" * "dy"/"dx" + "y" = tan "x"`
Solve the following differential equation:
`("x" + 2"y"^3) "dy"/"dx" = "y"`
Solve the following differential equation:
`"dy"/"dx" + "y" * sec "x" = tan "x"`
Solve the following differential equation:
`(1 - "x"^2) "dy"/"dx" + "2xy" = "x"(1 - "x"^2)^(1/2)`
Find the equation of the curve passing through the point `(3/sqrt2, sqrt2)` having a slope of the tangent to the curve at any point (x, y) is -`"4x"/"9y"`.
`(x + 2y^3 ) dy/dx = y`
The integrating factor of the differential equation sin y `("dy"/"dx")` = cos y(1 - x cos y) is ______.
Which of the following is a second order differential equation?
The solution of `(1 + x^2) ("d"y)/("d"x) + 2xy - 4x^2` = 0 is ______.
Let y = y(x) be a solution curve of the differential equation (y + 1)tan2xdx + tanxdy + ydx = 0, `x∈(0, π/2)`. If `lim_(x→0^+)` xy(x) = 1, then the value of `y(π/2)` is ______.
Let y = f(x) be a real-valued differentiable function on R (the set of all real numbers) such that f(1) = 1. If f(x) satisfies xf'(x) = x2 + f(x) – 2, then the area bounded by f(x) with x-axis between ordinates x = 0 and x = 3 is equal to ______.
Let the solution curve y = y(x) of the differential equation (4 + x2) dy – 2x (x2 + 3y + 4) dx = 0 pass through the origin. Then y (2) is equal to ______.
If the slope of the tangent at (x, y) to a curve passing through `(1, π/4)` is given by `y/x - cos^2(y/x)`, then the equation of the curve is ______.
If sin x is the integrating factor (IF) of the linear differential equation `dy/dx + Py` = Q then P is ______.
Solve the differential equation `dy/dx+2xy=x` by completing the following activity.
Solution: `dy/dx+2xy=x` ...(1)
This is the linear differential equation of the form `dy/dx +Py =Q,"where"`
`P=square` and Q = x
∴ `I.F. = e^(intPdx)=square`
The solution of (1) is given by
`y.(I.F.)=intQ(I.F.)dx+c=intsquare dx+c`
∴ `ye^(x^2) = square`
This is the general solution.
If sec x + tan x is the integrating factor of `dy/dx + Py` = Q, then value of P is ______.
