Advertisements
Advertisements
प्रश्न
Evaluate: `cos (sin^-1 (4/5) + sin^-1 (12/13))`
उत्तर
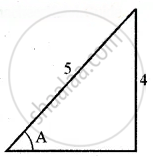
`sqrt(5^2 - 4^2)` = 3
cos A = `"Adj"/"Hyp" = 3/5`
Let `sin^-1 (4/5)` = A
sin A = `4/5`
∴ cos A = `3/5`
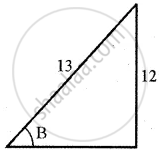
`sqrt(169 - 144) = sqrt 25` = 5
cos B = `"Adj"/"Hyp" = 5/13`
Let `sin^-1 (12/13)` = B
`12/13` = sin B
sin B = `12/13`
∴ cos B = `5/13`
Now `cos (sin^-1 (4/5) + sin^-1 (12/13))` = cos (A + B)
= cos A cos B – sin A sin B
`= 3/5 xx 5/13 - 4/5 xx 12/13`
`= 15/65 - 48/65`
`= - 33/65`
APPEARS IN
संबंधित प्रश्न
Evaluate the following:
`cot^-1{2cos(sin^-1 sqrt3/2)}`
Find the principal value of the following: tan- 1( - √3)
Evaluate the following:
`tan^-1(1) + cos^-1(1/2) + sin^-1(1/2)`
Evaluate the following:
`tan^-1 sqrt(3) - sec^-1 (-2)`
Show that `sin^-1(3/5) + sin^-1(8/17) = cos^-1(36/85)`
If `sin^-1(x/13) + cosec^-1(13/12) = pi/2`, then the value of x is ______
Prove that `cot(pi/4 - 2cot^-1 3)` = 7
Solve the following equation `cos(tan^-1x) = sin(cot^-1 3/4)`
If a = `(2sin theta)/(1 + costheta + sintheta)`, then `(1 + sintheta - costheta)/(1 + sintheta)` is
If sin–1a + sin–1b + sin–1c = π, then find the value of `asqrt(1 - a^2) + bsqrt(1 - b^2) + csqrt(1 - c^2)`.
