Advertisements
Advertisements
प्रश्न
Evaluate the following limits:
`lim_("h" -> 0) (sqrt(x + "h") - sqrt(x))/"h", x > 0`
उत्तर
`lim_("h" -> 0) (sqrt(x + "h") - sqrt(x))/"h", x > 0`
`lim_("h" -> 0) (sqrt(x + "h") - sqrt(x))/"h" = lim_(x + "h" -> x) ((x + "h")^(1/2) - x^(1/2))/((x + "h") - x)`
x + h → x
⇒ h → 0
`lim_(x -> "a") (x^"n" - "a"^"n")/(x - "a") = "na"^("n" - 1)`
= `1/2(x)^(1/2 - 1)`
= `1/2(x)^(-1/2)`
`lim_("h" -> 0) (sqrt(x + "h") - sqrt(x))/"h" = 1/2 xx 1/(x^(1/2))`
= `1/(2sqrt(x))`
APPEARS IN
संबंधित प्रश्न
Evaluate the following limit :
`lim_(x -> 1)[(x + x^2 + x^3 + ......... + x^"n" - "n")/(x - 1)]`
Evaluate the following limit :
`lim_(x -> 0)[(root(3)(1 + x) - sqrt(1 + x))/x]`
Evaluate the following :
Find the limit of the function, if it exists, at x = 1
f(x) = `{(7 - 4x, "for", x < 1),(x^2 + 2, "for", x ≥ 1):}`
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 2) f(x)` where `f(x) = {{:(4 - x",", x ≠ 2),(0",", x = 2):}`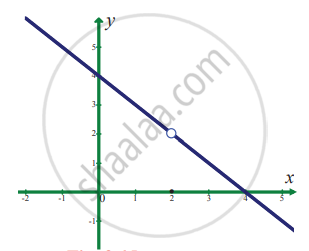
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 3) 1/(x - 3)`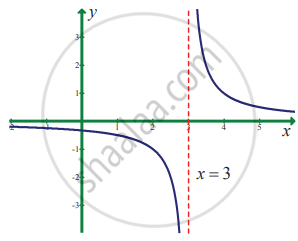
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 1) sin pi x`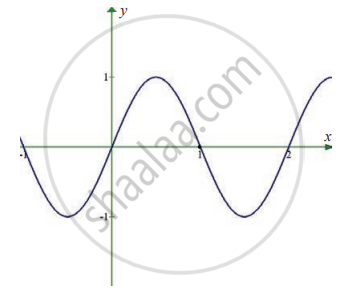
If f(2) = 4, can you conclude anything about the limit of f(x) as x approaches 2?
Verify the existence of `lim_(x -> 1) f(x)`, where `f(x) = {{:((|x - 1|)/(x - 1)",", "for" x ≠ 1),(0",", "for" x = 1):}`
Evaluate the following limits:
`lim_(sqrt(x) -> 3) (x^2 - 81)/(sqrt(x) - 3)`
Evaluate the following limits:
`lim_(x -> 1) (sqrt(x) - x^2)/(1 - sqrt(x))`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(1 + x) - 1)/x`
Evaluate the following limits:
`lim_(x-> 0) (1 - cos x)/x^2`
Evaluate the following limits:
`lim_(x -> pi) (1 + sinx)^(2"cosec"x)`
Choose the correct alternative:
`lim_(x -> 0) sqrt(1 - cos 2x)/x`
Choose the correct alternative:
`lim_(theta -> 0) (sinsqrt(theta))/(sqrt(sin theta)`
Choose the correct alternative:
If `lim_(x -> 0) (sin "p"x)/(tan 3x)` = 4, then the value of p is
`lim_(x→∞)((x + 7)/(x + 2))^(x + 4)` is ______.
