Advertisements
Advertisements
प्रश्न
Evaluate the following limit :
`lim_(x -> 0)[(root(3)(1 + x) - sqrt(1 + x))/x]`
उत्तर
`lim_(x -> 0)[(root(3)(1 + x) - sqrt(1 + x))/x]`
= `lim_(x -> 0) ((1 + x)^(1/3) - (1 + x)^(1/2))/x`
Put 1 + x = y ⇒ x = y − 1
As x→0, y→1
∴ `lim_(x -> 0) ((1 + x)^(1/3) - (1 + x)^(1/2))/x`
= `lim_(y -> 1) (y^(1/3) - y^(1/2))/(y - 1)`
= `lim_(y -> 1) ((y^(1/3) - 1) - (y^(1/2) - 1))/(y - 1)`
= `lim_(y -> 1) ((y^(1/3) - 1)/(y - 1) - y^(1/2 - 1)/(y - 1))`
= `lim_(y -> 1) (y^(1/3) - 1^(1/3))/(y - 1) - lim_(y -> 1) (y^(1/2) - 1^(1/2))/(y - 1)`
= `1/3(1)^(-(2)/3) - 1/2(1)^(-(1)/2) ...[because lim_(x -> "a") (x^"n" - "a"^"n")/(x - "a") = "na"^("n" - 1)]`
= `1/3 - 1/2`
= `(2 - 3)/6`
= `-1/6`
APPEARS IN
संबंधित प्रश्न
Evaluate the following limit :
`lim_(x -> 7)[((root(3)(x) - root(3)(7))(root(3)(x) + root(3)(7)))/(x - 7)]`
In the following example, given ∈ > 0, find a δ > 0 such that whenever, |x – a| < δ, we must have |f(x) – l| < ∈.
`lim_(x -> -3) (3x + 2)` = – 7
Evaluate the following :
`lim_(x -> 0)[x/(|x| + x^2)]`
Evaluate the following :
`lim_(x -> 0) {1/x^12 [1 - cos(x^2/2) - cos(x^4/4) + cos(x^2/2) cos(x^4/4)]}`
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> 0) (cos x - 1)/x`
| x | – 0.1 | – 0.01 | – 0.001 | 0.0001 | 0.01 | 0.1 |
| f(x) | 0.04995 | 0.0049999 | 0.0004999 | – 0.0004999 | – 0.004999 | – 0.04995 |
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 3) 1/(x - 3)`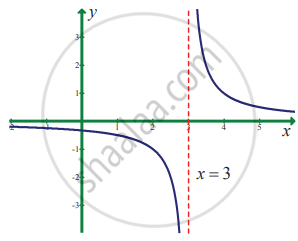
Sketch the graph of a function f that satisfies the given value:
f(0) is undefined
`lim_(x -> 0) f(x)` = 4
f(2) = 6
`lim_(x -> 2) f(x)` = 3
Write a brief description of the meaning of the notation `lim_(x -> 8) f(x)` = 25
Verify the existence of `lim_(x -> 1) f(x)`, where `f(x) = {{:((|x - 1|)/(x - 1)",", "for" x ≠ 1),(0",", "for" x = 1):}`
Evaluate the following limits:
`lim_(x -> 2) (x^4 - 16)/(x - 2)`
Evaluate the following limits:
`lim_(x ->) (x^"m" - 1)/(x^"n" - 1)`, m and n are integers
Evaluate the following limits:
`lim_(x -> 1) (root(3)(7 + x^3) - sqrt(3 + x^2))/(x - 1)`
Evaluate the following limits:
`lim_(x -> 2) (2 - sqrt(x + 2))/(root(3)(2) - root(3)(4 - x))`
Evaluate the following limits:
`lim_(x -> "a") (sqrt(x - "b") - sqrt("a" - "b"))/(x^2 - "a"^2) ("a" > "b")`
Evaluate the following limits:
`lim_(x -> 3) (x^2 - 9)/(x^2(x^2 - 6x + 9))`
Evaluate the following limits:
`lim_(x -> oo) 3/(x - 2) - (2x + 11)/(x^2 + x - 6)`
Evaluate the following limits:
`lim_(x ->oo) (x^3/(2x^2 - 1) - x^2/(2x + 1))`
An important problem in fishery science is to estimate the number of fish presently spawning in streams and use this information to predict the number of mature fish or “recruits” that will return to the rivers during the reproductive period. If S is the number of spawners and R the number of recruits, “Beverton-Holt spawner recruit function” is R(S) = `"S"/((alpha"S" + beta)` where `alpha` and `beta` are positive constants. Show that this function predicts approximately constant recruitment when the number of spawners is sufficiently large
Evaluate the following limits:
`lim_(x -> oo)(1 + 1/x)^(7x)`
Evaluate the following limits:
`lim_(x -> oo) ((2x^2 + 3)/(2x^2 + 5))^(8x^2 + 3)`
Evaluate the following limits:
`lim_(x -> oo) (1 + 3/x)^(x + 2)`
Evaluate the following limits:
`lim_(x -> 0) (sin^3(x/2))/x^2`
Evaluate the following limits:
`lim_(alpha -> 0) (sin(alpha^"n"))/(sin alpha)^"m"`
Evaluate the following limits:
`lim_(x -> 0) (sin("a" + x) - sin("a" - x))/x`
Evaluate the following limits:
`lim_(x -> 0) (1 - cos^2x)/(x sin2x)`
Evaluate the following limits:
`lim_(x -> oo) x [3^(1/x) + 1 - cos(1/x) - "e"^(1/x)]`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(2) - sqrt(1 + cosx))/(sin^2x)`
Choose the correct alternative:
`lim_(theta -> 0) (sinsqrt(theta))/(sqrt(sin theta)`
Choose the correct alternative:
`lim_(x -> 0) ("a"^x - "b"^x)/x` =
Choose the correct alternative:
`lim_(x -> 0) ("e"^tanx - "e"^x)/(tan x - x)` =
`lim_(x→0^+)(int_0^(x^2)(sinsqrt("t"))"dt")/x^3` is equal to ______.
The value of `lim_(x→0)(sin(ℓn e^x))^2/((e^(tan^2x) - 1))` is ______.
