Advertisements
Advertisements
प्रश्न
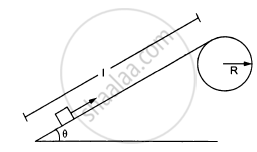
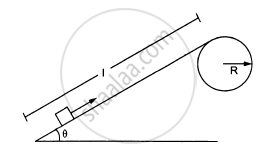
Figure ( following ) shows a smooth track which consists of a straight inclined part of length l joining smoothly with the circular part. A particle of mass m is projected up the incline from its bottom. Find the minimum projection-speed \[\nu_0\] for which the particle reaches the top of the track.
उत्तर
Net force on the particle at A and B \[F = \text{ mg }\sin \theta\] Work done to reach B from A, \[\text{W = FS = mg} \sin \theta \text{ l }\] Again, work done to reach B to C
\[= \text{mgh}\]
\[ = \text{mg R} \left( 1 - \cos \theta \right)\]
\[ = \text{mg}\left[ \text{l} \sin \theta + R \left( 1 - \cos \theta \right) \right]\]
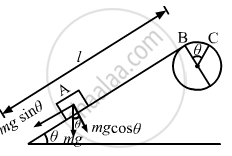
\[\Rightarrow \frac{1}{2}\text{m}\nu_2^2 = mg \left[ \text{l} \sin \theta + R \left( 1 - \cos \theta \right) \right]\]
\[ \Rightarrow \nu_2 = \sqrt{2g \left[ R \left( 1 - \cos \theta \right) + \text{l} \sin \theta \right]}\]
APPEARS IN
संबंधित प्रश्न
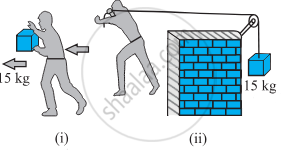
In Figure (i) the man walks 2 m carrying a mass of 15 kg on his hands. In Figure (ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater?
A ball is given a speed v on a rough horizontal surface. The ball travels through a distance l on the surface and stops. What is the work done by the kinetic friction?
The US athlete Florence Griffith-Joyner won the 100 m sprint gold medal at Seoul Olympics in 1988, setting a new Olympic record of 10⋅54 s. Assume that she achieved her maximum speed in a very short time and then ran the race with that speed till she crossed the line. Take her mass to be 50 kg. Calculate the kinetic energy of Griffith-Joyner at her full speed.
The US athlete Florence Griffith-Joyner won the 100 m sprint gold medal at Seoul Olympics in 1988, setting a new Olympic record of 10⋅54 s. Assume that she achieved her maximum speed in a very short time and then ran the race with that speed till she crossed the line. Take her mass to be 50 kg. Assuming that the track, wind etc. offered an average resistance of one-tenth of her weight, calculate the work done by the resistance during the run.
A water pump lifts water from 10 m below the ground. Water is pumped at a rate of 30 kg/minute with negligible velocity. Calculate the minimum horsepower that the engine should have to do this.
In a factory, 2000 kg of metal needs to be lifted by an engine through a distance of 12 m in 1 minute. Find the minimum horsepower of the engine to be used.
A scooter company gives the following specifications about its product:
Weight of the scooter − 95 kg
Maximum speed − 60 km/h
Maximum engine power − 3⋅5 hp
Pick up time to get the maximum speed − 5 s
Check the validity of these specifications.
A block of mass 100 g is moved with a speed of 5⋅0 m/s at the highest point in a closed circular tube of radius 10 cm kept in a vertical plane. The cross-section of the tube is such that the block just fits in it. The block makes several oscillations inside the tube and finally stops at the lowest point. Find the work done by the tube on the block during the process.
A small block of mass 200 g is kept at the top of a frictionless incline which is 10 m long and 3⋅2 m high. How much work was required (a) to lift the block from the ground and put it an the top, (b) to slide the block up the incline? What will be the speed of the block when it reaches the ground if (c) it falls off the incline and drops vertically to the ground (d) it slides down the incline? Take g = 10 m/s2.
A block of mass 5 kg is suspended from the end of a vertical spring which is stretched by 10 cm under the load of the block. The block is given a sharp impulse from below, so that it acquires an upward speed of 2 m/s. How high will it rise? Take g = 10 m/s2.
The bob of a stationary pendulum is given a sharp hit to impart it a horizontal speed of \[\sqrt{3 gl}\] . Find the angle rotated by the string before it becomes slack.
A heavy particle is suspended by a 1⋅5 m long string. It is given a horizontal velocity of \[\sqrt{57} \text{m/s}\] (a) Find the angle made by the string with the upward vertical when it becomes slack. (b) Find the speed of the particle at this instant. (c) Find the maximum height reached by the particle over the point of suspension. Take g = 10 m/s2.
Figure ( following ) shows a smooth track which consists of a straight inclined part of length l joining smoothly with the circular part. A particle of mass m is projected up the incline from its bottom. Assuming that the projection-speed is \[\nu_0\] and that the block does not lose contact with the track before reaching its top, find the force acting on it when it reaches the top.
An electron and a proton are moving under the influence of mutual forces. In calculating the change in the kinetic energy of the system during motion, one ignores the magnetic force of one on another. This is because ______.
A man, of mass m, standing at the bottom of the staircase, of height L climbs it and stands at its top.
- Work done by all forces on man is equal to the rise in potential energy mgL.
- Work done by all forces on man is zero.
- Work done by the gravitational force on man is mgL.
- The reaction force from a step does not do work because the point of application of the force does not move while the force exists.
Give example of a situation in which an applied force does not result in a change in kinetic energy.
A rocket accelerates straight up by ejecting gas downwards. In a small time interval ∆t, it ejects a gas of mass ∆m at a relative speed u. Calculate KE of the entire system at t + ∆t and t and show that the device that ejects gas does work = `(1/2)∆m u^2` in this time interval (neglect gravity).
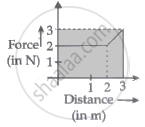
A particle moves in one dimension from rest under the influence of a force that varies with the distance travelled by the particle as shown in the figure. The kinetic energy of the particle after it has travelled 3 m is ______.