Advertisements
Advertisements
प्रश्न
Find the foot of the perpendicular from (0, 2, 7) on the line \[\frac{x + 2}{- 1} = \frac{y - 1}{3} = \frac{z - 3}{- 2} .\]
Advertisements
उत्तर
Let L be the foot of the perpendicular drawn from the point P (0, 2, 7) to the given line.
The coordinates of a general point on the line \[\frac{x + 2}{- 1} = \frac{y - 1}{3} = \frac{z - 3}{- 2}\] are given by
\[\frac{x + 2}{- 1} = \frac{y - 1}{3} = \frac{z - 3}{- 2} = \lambda\]
\[ \Rightarrow x = - \lambda - 2\]
\[ y = 3\lambda + 1 \]
\[ z = - 2\lambda + 3\]
Let the coordinates of L be \[\left( - \lambda - 2, 3\lambda + 1, - 2\lambda + 3 \right)\]
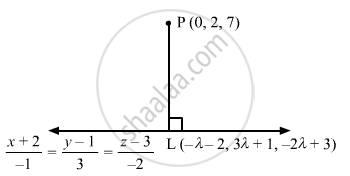
The direction ratios of PL are proportional to \[- \lambda - 2 - 0, 3\lambda + 1 - 2, - 2\lambda + 3 - 7, i . e . - \lambda - 2, 3\lambda - 1, - 2\lambda - 4\]
The direction ratios of the given line are proportional to -1,3,-2, but PL is perpendicular to the given line.
\[\therefore - 1\left( - \lambda - 2 \right) + 3\left( 3\lambda - 1 \right) - 2\left( - 2\lambda - 4 \right) = 0\]
\[ \Rightarrow \lambda = - \frac{1}{2}\]
Substituting \[\lambda = - \frac{1}{2}\] in \[\left( - \lambda - 2, 3\lambda + 1, - 2\lambda + 3 \right)\]
we get the coordinates of L as \[\left( - \frac{3}{2}, - \frac{1}{2}, 4 \right)\]
APPEARS IN
संबंधित प्रश्न
The Cartesian equations of line are 3x+1=6y-2=1-z find its equation in vector form.
The Cartestation equation of line is `(x-6)/2=(y+4)/7=(z-5)/3` find its vector equation.
If the Cartesian equations of a line are ` (3-x)/5=(y+4)/7=(2z-6)/4` , write the vector equation for the line.
Show that the line through the points (1, −1, 2) (3, 4, −2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).
Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector `3hati+2hatj-2hatk`.
The Cartesian equation of a line is `(x-5)/3 = (y+4)/7 = (z-6)/2` Write its vector form.
Find the vector and the Cartesian equations of the lines that pass through the origin and (5, −2, 3).
Find the vector equation of a line which is parallel to the vector \[2 \hat{i} - \hat{j} + 3 \hat{k}\] and which passes through the point (5, −2, 4). Also, reduce it to cartesian form.
The cartesian equations of a line are \[\frac{x - 5}{3} = \frac{y + 4}{7} = \frac{z - 6}{2} .\] Find a vector equation for the line.
Find the vector equation of a line passing through the point with position vector \[\hat{i} - 2 \hat{j} - 3 \hat{k}\] and parallel to the line joining the points with position vectors \[\hat{i} - \hat{j} + 4 \hat{k} \text{ and } 2 \hat{i} + \hat{j} + 2 \hat{k} .\] Also, find the cartesian equivalent of this equation.
Find the points on the line \[\frac{x + 2}{3} = \frac{y + 1}{2} = \frac{z - 3}{2}\] at a distance of 5 units from the point P (1, 3, 3).
Find the angle between the following pair of line:
\[\frac{x - 5}{1} = \frac{2y + 6}{- 2} = \frac{z - 3}{1} \text{ and } \frac{x - 2}{3} = \frac{y + 1}{4} = \frac{z - 6}{5}\]
Find the angle between the following pair of line:
\[\frac{- x + 2}{- 2} = \frac{y - 1}{7} = \frac{z + 3}{- 3} \text{ and } \frac{x + 2}{- 1} = \frac{2y - 8}{4} = \frac{z - 5}{4}\]
Find the angle between two lines, one of which has direction ratios 2, 2, 1 while the other one is obtained by joining the points (3, 1, 4) and (7, 2, 12).
Find the equations of the line passing through the point (2, 1, 3) and perpendicular to the lines \[\frac{x - 1}{1} = \frac{y - 2}{2} = \frac{z - 3}{3} \text{ and } \frac{x}{- 3} = \frac{y}{2} = \frac{z}{5}\]
Determine whether the following pair of lines intersect or not:
\[\overrightarrow{r} = \left( \hat{i} - \hat{j} \right) + \lambda\left( 2 \hat{i} + \hat{k} \right) \text{ and } \overrightarrow{r} = \left( 2 \hat{i} - \hat{j} \right) + \mu\left( \hat{i} + \hat{j} - \hat{k} \right)\]
Determine whether the following pair of lines intersect or not:
\[\frac{x - 1}{2} = \frac{y + 1}{3} = z \text{ and } \frac{x + 1}{5} = \frac{y - 2}{1}; z = 2\]
Show that the lines \[\vec{r} = 3 \hat{i} + 2 \hat{j} - 4 \hat{k} + \lambda\left( \hat{i} + 2 \hat{j} + 2 \hat{k} \right) \text{ and } \vec{r} = 5 \hat{i} - 2 \hat{j} + \mu\left( 3 \hat{i} + 2 \hat{j} + 6 \hat{k} \right)\] are intersecting. Hence, find their point of intersection.
Find the coordinates of the foot of perpendicular drawn from the point A(1, 8, 4) to the line joining the points B(0, −1, 3) and C(2, −3, −1).
Find the shortest distance between the following pairs of lines whose vector equations are: \[\overrightarrow{r} = \left( 3 \hat{i} + 5 \hat{j} + 7 \hat{k} \right) + \lambda\left( \hat{i} - 2 \hat{j} + 7 \hat{k} \right) \text{ and } \overrightarrow{r} = - \hat{i} - \hat{j} - \hat{k} + \mu\left( 7 \hat{i} - 6 \hat{j} + \hat{k} \right)\]
Find the shortest distance between the following pairs of lines whose vector equations are: \[\overrightarrow{r} = \left( 1 - t \right) \hat{i} + \left( t - 2 \right) \hat{j} + \left( 3 - t \right) \hat{k} \text{ and } \overrightarrow{r} = \left( s + 1 \right) \hat{i} + \left( 2s - 1 \right) \hat{j} - \left( 2s + 1 \right) \hat{k} \]
Find the shortest distance between the following pairs of lines whose cartesian equations are: \[\frac{x - 3}{1} = \frac{y - 5}{- 2} = \frac{z - 7}{1} \text{ and } \frac{x + 1}{7} = \frac{y + 1}{- 6} = \frac{z + 1}{1}\]
Find the shortest distance between the lines \[\overrightarrow{r} = \hat{i} + 2 \hat{j} + 3 \hat{k} + \lambda\left( \hat{i} - 3 \hat{j} + 2 \hat{k} \right) \text{ and } \overrightarrow{r} = 4 \hat{i} + 5 \hat{j} + 6 \hat{k} + \mu\left( 2 \hat{i} + 3 \hat{j} + \hat{k} \right)\]
Find the distance between the lines l1 and l2 given by \[\overrightarrow{r} = \hat{i} + 2 \hat{j} - 4 \hat{k} + \lambda\left( 2 \hat{i} + 3 \hat{j} + 6 \hat{k} \right) \text{ and } , \overrightarrow{r} = 3 \hat{i} + 3 \hat{j} - 5 \hat{k} + \mu\left( 2 \hat{i} + 3 \hat{j} + 6 \hat{k} \right)\]
Cartesian equations of a line AB are \[\frac{2x - 1}{2} = \frac{4 - y}{7} = \frac{z + 1}{2} .\] Write the direction ratios of a line parallel to AB.
Find the Cartesian equations of the line which passes through the point (−2, 4 , −5) and is parallel to the line \[\frac{x + 3}{3} = \frac{4 - y}{5} = \frac{z + 8}{6} .\]
Find the angle between the lines
\[\vec{r} = \left( 2 \hat{i} - 5 \hat{j} + \hat{k} \right) + \lambda\left( 3 \hat{i} + 2 \hat{j} + 6 \hat{k} \right)\] and \[\vec{r} = 7 \hat{i} - 6 \hat{k} + \mu\left( \hat{i} + 2 \hat{j} + 2 \hat{k} \right)\]
The angle between the straight lines \[\frac{x + 1}{2} = \frac{y - 2}{5} = \frac{z + 3}{4} and \frac{x - 1}{1} = \frac{y + 2}{2} = \frac{z - 3}{- 3}\] is
The lines `x/1 = y/2 = z/3 and (x - 1)/-2 = (y - 2)/-4 = (z - 3)/-6` are
The direction ratios of the line perpendicular to the lines \[\frac{x - 7}{2} = \frac{y + 17}{- 3} = \frac{z - 6}{1} \text{ and }, \frac{x + 5}{1} = \frac{y + 3}{2} = \frac{z - 4}{- 2}\] are proportional to
The angle between the lines
If a line makes angles α, β and γ with the axes respectively, then cos 2 α + cos 2 β + cos 2 γ =
The straight line \[\frac{x - 3}{3} = \frac{y - 2}{1} = \frac{z - 1}{0}\] is
Choose correct alternatives:
The difference between the slopes of the lines represented by 3x2 - 4xy + y2 = 0 is 2
Find the cartesian equation of the line which passes ·through the point (– 2, 4, – 5) and parallel to the line given by.
`(x + 3)/3 = (y - 4)/5 = (z + 8)/6`
Find the vector equation of a line passing through a point with position vector `2hati - hatj + hatk` and parallel to the line joining the points `-hati + 4hatj + hatk` and `-hati + 2hatj + 2hatk`.
The lines `(x - 1)/2 = (y + 1)/2 = (z - 1)/4` and `(x - 3)/1 = (y - k)/2 = z/1` intersect each other at point
