Advertisements
Advertisements
प्रश्न
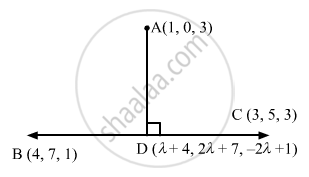
Find the foot of the perpendicular drawn from the point A (1, 0, 3) to the joint of the points B (4, 7, 1) and C (3, 5, 3).
उत्तर
Let D be the foot of the perpendicular drawn from the point A (1, 0, 3) to the line BC.
The coordinates of a general point on the line BC are given by
\[\frac{x - 4}{4 - 3} = \frac{y - 7}{7 - 5} = \frac{z - 1}{1 - 3} = \lambda\]
\[ \Rightarrow x = \lambda + 4\]
\[ y = 2\lambda + 7 \]
\[ z = - 2\lambda + 1\]
Let the coordinates of D be
\[\left( \lambda + 4, 2\lambda + 7, - 2\lambda + 1 \right)\]
The direction ratios of AD are proportional to
\[\lambda + 4 - 1, 2\lambda + 7 - 0, - 2\lambda + 1 - 3, i . e . \lambda + 3, 2\lambda + 7, - 2\lambda - 2\]
The direction ratios of the line BC are proportional to 1, 2,-2, but AD is perpendicular to the line BC.
\[\therefore 1\left( \lambda + 3 \right) + 2\left( 2\lambda + 7 \right) - 2\left( - 2\lambda - 2 \right) = 0\]
\[ \Rightarrow \lambda = - \frac{7}{3}\]
Substituting
\[ \Rightarrow \lambda = - \frac{7}{3}\] in
\[\left( \lambda + 4, 2\lambda + 7, - 2\lambda + 1 \right)\] we get the coordinates of D as \[\left( \frac{5}{3}, \frac{7}{3}, \frac{17}{3} \right)\] .
APPEARS IN
संबंधित प्रश्न
Find the coordinates of the point where the line through the points A(3, 4, 1) and B(5, 1, 6) crosses the XZ plane. Also find the angle which this line makes with the XZ plane.
Show that the three lines with direction cosines `12/13, (-3)/13, (-4)/13; 4/13, 12/13, 3/13; 3/13, (-4)/13, 12/13 ` are mutually perpendicular.
Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector `3hati+2hatj-2hatk`.
Find the vector and the Cartesian equations of the line that passes through the points (3, −2, −5), (3, −2, 6).
A line passes through the point with position vector \[2 \hat{i} - 3 \hat{j} + 4 \hat{k} \] and is in the direction of \[3 \hat{i} + 4 \hat{j} - 5 \hat{k} .\] Find equations of the line in vector and cartesian form.
ABCD is a parallelogram. The position vectors of the points A, B and C are respectively, \[4 \hat{ i} + 5 \hat{j} -10 \hat{k} , 2 \hat{i} - 3 \hat{j} + 4 \hat{k} \text{ and } - \hat{i} + 2 \hat{j} + \hat{k} .\] Find the vector equation of the line BD. Also, reduce it to cartesian form.
The cartesian equations of a line are \[\frac{x - 5}{3} = \frac{y + 4}{7} = \frac{z - 6}{2} .\] Find a vector equation for the line.
Find the angle between the following pair of line:
\[\frac{x - 2}{3} = \frac{y + 3}{- 2}, z = 5 \text{ and } \frac{x + 1}{1} = \frac{2y - 3}{3} = \frac{z - 5}{2}\]
Find the angle between the following pair of line:
\[\frac{- x + 2}{- 2} = \frac{y - 1}{7} = \frac{z + 3}{- 3} \text{ and } \frac{x + 2}{- 1} = \frac{2y - 8}{4} = \frac{z - 5}{4}\]
Find the angle between the pairs of lines with direction ratios proportional to 2, 2, 1 and 4, 1, 8 .
Find the angle between the pairs of lines with direction ratios proportional to 1, 2, −2 and −2, 2, 1 .
Find the equations of the line passing through the point (−1, 2, 1) and parallel to the line \[\frac{2x - 1}{4} = \frac{3y + 5}{2} = \frac{2 - z}{3} .\]
Find the equation of the line passing through the point (2, −1, 3) and parallel to the line \[\overrightarrow{r} = \left( \hat{i} - 2 \hat{j} + \hat{k} \right) + \lambda\left( 2 \hat{i} + 3 \hat{j} - 5 \hat{k} \right) .\]
Find the equations of the line passing through the point (2, 1, 3) and perpendicular to the lines \[\frac{x - 1}{1} = \frac{y - 2}{2} = \frac{z - 3}{3} \text{ and } \frac{x}{- 3} = \frac{y}{2} = \frac{z}{5}\]
Show that the lines \[\frac{x - 5}{7} = \frac{y + 2}{- 5} = \frac{z}{1} \text{ and } \frac{x}{1} = \frac{y}{2} = \frac{z}{3}\] are perpendicular to each other.
Show that the lines \[\vec{r} = 3 \hat{i} + 2 \hat{j} - 4 \hat{k} + \lambda\left( \hat{i} + 2 \hat{j} + 2 \hat{k} \right) \text{ and } \vec{r} = 5 \hat{i} - 2 \hat{j} + \mu\left( 3 \hat{i} + 2 \hat{j} + 6 \hat{k} \right)\] are intersecting. Hence, find their point of intersection.
Find the length of the perpendicular drawn from the point (5, 4, −1) to the line \[\overrightarrow{r} = \hat{i} + \lambda\left( 2 \hat{i} + 9 \hat{j} + 5 \hat{k} \right) .\]
Find the foot of the perpendicular drawn from the point \[\hat{i} + 6 \hat{j} + 3 \hat{k} \] to the line \[\overrightarrow{r} = \hat{j} + 2 \hat{k} + \lambda\left( \hat{i} + 2 \hat{j} + 3 \hat{k} \right) .\] Also, find the length of the perpendicular
Find the equation of the perpendicular drawn from the point P (−1, 3, 2) to the line \[\overrightarrow{r} = \left( 2 \hat{j} + 3 \hat{k} \right) + \lambda\left( 2 \hat{i} + \hat{j} + 3 \hat{k} \right) .\] Also, find the coordinates of the foot of the perpendicular from P.
Find the foot of the perpendicular from (0, 2, 7) on the line \[\frac{x + 2}{- 1} = \frac{y - 1}{3} = \frac{z - 3}{- 2} .\]
Find the shortest distance between the following pairs of lines whose vector equations are: \[\overrightarrow{r} = \left( 1 - t \right) \hat{i} + \left( t - 2 \right) \hat{j} + \left( 3 - t \right) \hat{k} \text{ and } \overrightarrow{r} = \left( s + 1 \right) \hat{i} + \left( 2s - 1 \right) \hat{j} - \left( 2s + 1 \right) \hat{k} \]
Find the shortest distance between the following pairs of lines whose vector equations are: \[\overrightarrow{r} = \left( 8 + 3\lambda \right) \hat{i} - \left( 9 + 16\lambda \right) \hat{j} + \left( 10 + 7\lambda \right) \hat{k} \]\[\overrightarrow{r} = 15 \hat{i} + 29 \hat{j} + 5 \hat{k} + \mu\left( 3 \hat{i} + 8 \hat{j} - 5 \hat{k} \right)\]
Find the shortest distance between the following pairs of lines whose cartesian equations are : \[\frac{x - 1}{2} = \frac{y + 1}{3} = z \text{ and } \frac{x + 1}{3} = \frac{y - 2}{1}; z = 2\]
By computing the shortest distance determine whether the following pairs of lines intersect or not: \[\overrightarrow{r} = \left( \hat{i} + \hat{j} - \hat{k} \right) + \lambda\left( 3 \hat{i} - \hat{j} \right) \text{ and } \overrightarrow{r} = \left( 4 \hat{i} - \hat{k} \right) + \mu\left( 2 \hat{i} + 3 \hat{k} \right)\]
By computing the shortest distance determine whether the following pairs of lines intersect or not: \[\frac{x - 5}{4} = \frac{y - 7}{- 5} = \frac{z + 3}{- 5} \text{ and } \frac{x - 8}{7} = \frac{y - 7}{1} = \frac{z - 5}{3}\]
Write the direction cosines of the line whose cartesian equations are 6x − 2 = 3y + 1 = 2z − 4.
Write the angle between the lines 2x = 3y = −z and 6x = −y = −4z.
The cartesian equations of a line AB are \[\frac{2x - 1}{\sqrt{3}} = \frac{y + 2}{2} = \frac{z - 3}{3} .\] Find the direction cosines of a line parallel to AB.
If the equations of a line AB are
\[\frac{3 - x}{1} = \frac{y + 2}{- 2} = \frac{z - 5}{4},\] write the direction ratios of a line parallel to AB.
The direction ratios of the line x − y + z − 5 = 0 = x − 3y − 6 are proportional to
The perpendicular distance of the point P (1, 2, 3) from the line \[\frac{x - 6}{3} = \frac{y - 7}{2} = \frac{z - 7}{- 2}\] is
If the direction ratios of a line are proportional to 1, −3, 2, then its direction cosines are
The projections of a line segment on X, Y and Z axes are 12, 4 and 3 respectively. The length and direction cosines of the line segment are
Find the value of p for which the following lines are perpendicular :
`(1-x)/3 = (2y-14)/(2p) = (z-3)/2 ; (1-x)/(3p) = (y-5)/1 = (6-z)/5`
If y – 2x – k = 0 touches the conic 3x2 – 5y2 = 15, find the value of k.
Choose correct alternatives:
The difference between the slopes of the lines represented by 3x2 - 4xy + y2 = 0 is 2
The equation 4x2 + 4xy + y2 = 0 represents two ______
Find the vector equation of a line passing through a point with position vector `2hati - hatj + hatk` and parallel to the line joining the points `-hati + 4hatj + hatk` and `-hati + 2hatj + 2hatk`.
Equation of a line passing through (1, 1, 1) and parallel to z-axis is ______.
