Advertisements
Advertisements
प्रश्न
Find k, if R(1, –1), S (–2, k) and slope of line RS is –2.
उत्तर
Slope of line RS is –2
Slope of RS will be
\[\frac{y_2 - y_1}{x_2 - x_1} = \frac{k - \left( - 1 \right)}{- 2 - 1} = \frac{k + 1}{- 3} = - 2\]
\[ \Rightarrow k + 1 = 6\]
\[ \Rightarrow k = 5\]
APPEARS IN
संबंधित प्रश्न
A slope of a line is 3 and y-intercept is –4. Write the equation of a line
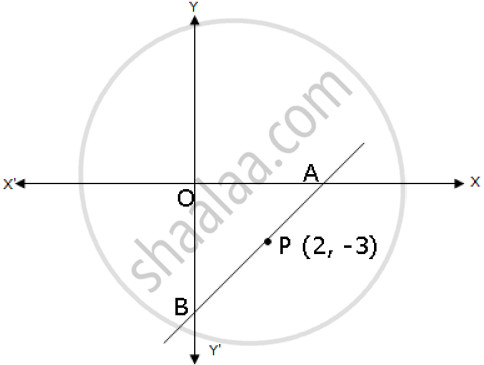
A and B are two points on the x-axis and y-axis respectively. P (2, −3) is the midpoint of AB. Find the:
(1) coordinates of A and B
(2) slope of line AB.
(3) an equation of line AB.
Without using the distance formula, show that the points A(4, −2), B(−4, 4) and C(10, 6) are the vertices of a right-angled triangle.
Find the slope and the inclination of the line AB if : A = `(-1, 2sqrt(3))` and B = `(-2, sqrt(3))`
Lines mx + 3y + 7 = 0 and 5x – ny – 3 = 0 are perpendicular to each other. Find the relation connecting m and n.
If the lines y = 3x + 7 and 2y + px = 3 are perpendicular to each other, find the value of p.
The line through A(−2, 3) and B(4, b) is perpendicular to the line 2x – 4y = 5. Find the value of b.
Find the slope of the lines passing through the given point.
P (–3, 1) , Q (5, –2)
Find the slope of the lines passing through the given point.
C (5, –2) , D (7, 3)
Determine whether the following point is collinear.
A(–1, –1), B(0, 1), C(1, 3)
Determine whether the given point is collinear.
A (0, 2), B (1, -0.5), C (2, -3)
Show that the line joining the points A(4, 8) and B(5, 5) is parallel to the line joining the points C(2, 4) and D(1, 7).
Find the slope of a line passing through the given pair of points (3,7) and (5,13)
Find the slope and the y-intercept of the following line 2x + 3y = 12
Verify whether the following points are collinear or not:
A(1, –3), B(2, –5), C(–4, 7).
Find the slope of the line passing through the points M(4,0) and N(-2,-3).
Find the slope of the line passing through the points A(4,7) and B(2,3).
Find the value, of k, if the line represented by kx – 5y + 4 = 0 and 4x – 2y + 5 = 0 are perpendicular to each other.
Four alternative answers for the following question are given. Choose the correct alternative and write its alphabet:
Slope of X-axis is ______.
