Advertisements
Advertisements
प्रश्न
Find the maximum angular speed of the electron of a hydrogen atom in a stationary orbit.
उत्तर
Let the mass of the electron be m.
Let the radius of the hydrogen's first stationary orbit be r.
Let the linear speed and the angular speed of the electron be v and ω, respectively.
According to the Bohr's theory, angular momentum (L) of the electron is an integral multiple of h/2 `pi`, where h is the Planck's constant.
`rArr mvr= (nh)/(2pi)` (Here , n is an integer)
V = rω
`⇒ mr^2 omega = (nh)/(2pi)`
`⇒ omega = (nh)/(2pixxmxxr^2)`
`therefore omega = (1xx(6.63xx10^34))/(2xx(3.14)xx(9.1093xx10^-31)xx(0.53xx10^-10)^2`
`= 0.413 xx 10^17 (rad)//s = 4.13 xx 10^16 (rad)//s`
APPEARS IN
संबंधित प्रश्न
Classically, an electron can be in any orbit around the nucleus of an atom. Then what determines the typical atomic size? Why is an atom not, say, a thousand times bigger than its typical size? The question had greatly puzzled Bohr before he arrived at his famous model of the atom that you have learnt in the text. To simulate what he might well have done before his discovery, let us play as follows with the basic constants of nature and see if we can get a quantity with the dimensions of length that is roughly equal to the known size of an atom (~ 10−10 m).
(a) Construct a quantity with the dimensions of length from the fundamental constants e, me, and c. Determine its numerical value.
(b) You will find that the length obtained in (a) is many orders of magnitude smaller than the atomic dimensions. Further, it involves c. But energies of atoms are mostly in non-relativistic domain where c is not expected to play any role. This is what may have suggested Bohr to discard c and look for ‘something else’ to get the right atomic size. Now, the Planck’s constant h had already made its appearance elsewhere. Bohr’s great insight lay in recognising that h, me, and e will yield the right atomic size. Construct a quantity with the dimension of length from h, me, and e and confirm that its numerical value has indeed the correct order of magnitude.
The minimum orbital angular momentum of the electron in a hydrogen atom is
In which of the following transitions will the wavelength be minimum?
In which of the following systems will the radius of the first orbit (n = 1) be minimum?
Which of the following curves may represent the speed of the electron in a hydrogen atom as a function of trincipal quantum number n?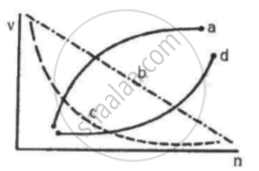
The radius of the shortest orbit in a one-electron system is 18 pm. It may be
A hydrogen atom in ground state absorbs 10.2 eV of energy. The orbital angular momentum of the electron is increased by
Let An be the area enclosed by the nth orbit in a hydrogen atom. The graph of ln (An/A1) against ln(n)
(a) will pass through the origin
(b) will be a straight line with slope 4
(c) will be a monotonically increasing nonlinear curve
(d) will be a circle
Calculate the smallest wavelength of radiation that may be emitted by (a) hydrogen, (b) He+ and (c) Li++.
Find the radius and energy of a He+ ion in the states (a) n = 1, (b) n = 4 and (c) n = 10.
A hydrogen atom in a state having a binding energy of 0.85 eV makes transition to a state with excitation energy 10.2 e.V (a) Identify the quantum numbers n of the upper and the lower energy states involved in the transition. (b) Find the wavelength of the emitted radiation.
What is the energy of a hydrogen atom in the first excited state if the potential energy is taken to be zero in the ground state?
Suppose, in certain conditions only those transitions are allowed to hydrogen atoms in which the principal quantum number n changes by 2. (a) Find the smallest wavelength emitted by hydrogen. (b) List the wavelength emitted by hydrogen in the visible range (380 nm to 780 nm).
The average kinetic energy of molecules in a gas at temperature T is 1.5 kT. Find the temperature at which the average kinetic energy of the molecules of hydrogen equals the binding energy of its atoms. Will hydrogen remain in molecular from at this temperature? Take k = 8.62 × 10−5 eV K−1.
Show that the ratio of the magnetic dipole moment to the angular momentum (l = mvr) is a universal constant for hydrogen-like atoms and ions. Find its value.
When a photon is emitted from an atom, the atom recoils. The kinetic energy of recoil and the energy of the photon come from the difference in energies between the states involved in the transition. Suppose, a hydrogen atom changes its state from n = 3 to n = 2. Calculate the fractional change in the wavelength of light emitted, due to the recoil.
Positronium is just like a H-atom with the proton replaced by the positively charged anti-particle of the electron (called the positron which is as massive as the electron). What would be the ground state energy of positronium?
In the Auger process an atom makes a transition to a lower state without emitting a photon. The excess energy is transferred to an outer electron which may be ejected by the atom. (This is called an Auger electron). Assuming the nucleus to be massive, calculate the kinetic energy of an n = 4 Auger electron emitted by Chromium by absorbing the energy from a n = 2 to n = 1 transition.
