Advertisements
Advertisements
प्रश्न
Find the distance between the origin and the point:
(8, -15)
उत्तर
Coordinates of origin are O (0, 0).
C (8, -15)
CO = `sqrt((0 - 8)^2 + (0 + 15)^2)`
= `sqrt(64 + 225)`
= `sqrt(289)`
= 17
APPEARS IN
संबंधित प्रश्न
The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q(2, –5) and R(–3, 6), find the coordinates of P.
Name the type of quadrilateral formed, if any, by the following point, and give reasons for your answer:
(−3, 5), (3, 1), (0, 3), (−1, −4)
If Q (0, 1) is equidistant from P (5, − 3) and R (x, 6), find the values of x. Also find the distance QR and PR.
Two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of other two
vertices.
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is ______.
Find the distance between the following point :
(sec θ , tan θ) and (- tan θ , sec θ)
ABCD is a square . If the coordinates of A and C are (5 , 4) and (-1 , 6) ; find the coordinates of B and D.
What point on the x-axis is equidistant from the points (7, 6) and (-3, 4)?
A point P lies on the x-axis and another point Q lies on the y-axis.
If the abscissa of point P is -12 and the ordinate of point Q is -16; calculate the length of line segment PQ.
Find distance between points O(0, 0) and B(– 5, 12)
Show that P(– 2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle
Show that A(1, 2), (1, 6), C(1 + 2 `sqrt(3)`, 4) are vertices of a equilateral triangle
AOBC is a rectangle whose three vertices are A(0, 3), O(0, 0) and B(5, 0). The length of its diagonal is ______.
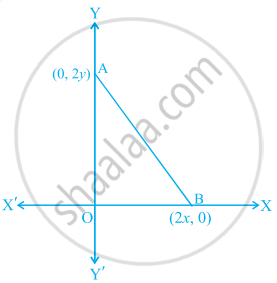
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is ______.
A circle drawn with origin as the centre passes through `(13/2, 0)`. The point which does not lie in the interior of the circle is ______.
The equation of the perpendicular bisector of line segment joining points A(4,5) and B(-2,3) is ______.
Points A(4, 3), B(6, 4), C(5, –6) and D(–3, 5) are the vertices of a parallelogram.
A circle has its centre at the origin and a point P(5, 0) lies on it. The point Q(6, 8) lies outside the circle.
The point P(–2, 4) lies on a circle of radius 6 and centre C(3, 5).
|
Case Study Trigonometry in the form of triangulation forms the basis of navigation, whether it is by land, sea or air. GPS a radio navigation system helps to locate our position on earth with the help of satellites. |
- Make a labelled figure on the basis of the given information and calculate the distance of the boat from the foot of the observation tower.
- After 10 minutes, the guard observed that the boat was approaching the tower and its distance from tower is reduced by 240(`sqrt(3)` - 1) m. He immediately raised the alarm. What was the new angle of depression of the boat from the top of the observation tower?

