Advertisements
Advertisements
प्रश्न
Find the feasible solution for the following system of linear inequations:
0 ≤ x ≤ 3, 0 ≤ y ≤ 3, x + y ≤ 5, 2x + y ≥ 4
उत्तर
First we draw the lines AB, CD, EF and GH whose equations are x + y = 5, 2x + y = 4, x = 3 and y = 3 respectively.
| Line | Equation | Points on the X-axis | Points on the Y-axis | Sign | Region |
| AB | x + y = 5 | A(5, 0) | B(0, 5) | ≤ | origin side of line AB |
| CD | 2x + y = 4 | C(2, 0) | D(0, 4) | ≥ | non-origin side of line CD |
| EF | x = 3 | E(3, 0) | - | ≤ | origin side of line EF |
| GH | y = 3 | - | H(0, 3) | ≤ | origin side of line GH |
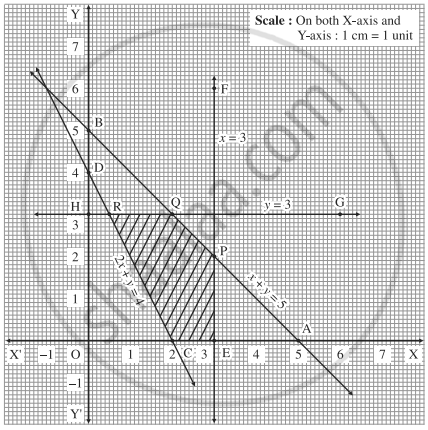
The feasible solution is CEPQRC which is shaded in the graph.
संबंधित प्रश्न
The equations given of the two regression lines are 2x + 3y - 6 = 0 and 5x + 7y - 12 = 0.
Find:
(a) Correlation coefficient
(b) `sigma_x/sigma_y`
Given that the observations are: (9, -4), (10, -3), (11, -1), (12, 0), (13, 1), (14, 3), (15, 5), (16, 8). Find the two lines of regression and estimate the value of y when x = 13·5.
Identify the regression equations of X on Y and Y on X from the following equations :
2x + 3y = 6 and 5x + 7y – 12 = 0
Find the equation of the regression line of y on x, if the observations (x, y) are as follows :
(1,4),(2,8),(3,2),(4,12),(5,10),(6,14),(7,16),(8,6),(9,18)
Also, find the estimated value of y when x = 14.
If Σx1 = 56 Σy1 = 56, Σ`x_1^2` = 478,
Σ`y_1^2` = 476, Σx1y1 = 469 and n = 7, Find
(a) the regression equation of y on x.
(b) y, if x = 12.
Find graphical solution for following system of linear inequations :
3x + 2y ≤ 180; x+ 2y ≤ 120, x ≥ 0, y ≥ 0
Hence find co-ordinates of corner points of the common region.
Information on v:ehicles [in thousands) passing through seven different highways during a day (X) and number of accidents reported (Y) is given as follows :
`Sigmax_i` = 105, `Sigmay_i` = 409, n = 7, `Sigmax_i^2` = 1681, `Sigmay_i^2` = 39350 `Sigmax_iy_i` = 8075
Obtain the linear regression of Y on X.
Calculate the Spearman’s rank correlation coefficient for the following data and interpret the result:
| X | 35 | 54 | 80 | 95 | 73 | 73 | 35 | 91 | 83 | 81 |
| Y | 40 | 60 | 75 | 90 | 70 | 75 | 38 | 95 | 75 | 70 |
For the following bivariate data obtain the equations of two regression lines:
| X | 1 | 2 | 3 | 4 | 5 |
| Y | 5 | 7 | 9 | 11 | 13 |
From the data of 20 pairs of observations on X and Y, following results are obtained.
`barx` = 199, `bary` = 94,
`sum(x_i - barx)^2` = 1200, `sum(y_i - bary)^2` = 300,
`sum(x_i - bar x)(y_i - bar y)` = –250
Find:
- The line of regression of Y on X.
- The line of regression of X on Y.
- Correlation coefficient between X and Y.
Given the following data, obtain a linear regression estimate of X for Y = 10, `bar x = 7.6, bar y = 14.8, sigma_x = 3.2, sigma_y = 16` and r = 0.7
bYX is ______.
The data obtained on X, the length of time in weeks that a promotional project has been in progress at a small business, and Y, the percentage increase in weekly sales over the period just prior to the beginning of the campaign.
| X | 1 | 2 | 3 | 4 | 1 | 3 | 1 | 2 | 3 | 4 | 2 | 4 |
| Y | 10 | 10 | 18 | 20 | 11 | 15 | 12 | 15 | 17 | 19 | 13 | 16 |
Find the equation of the regression line to predict the percentage increase in sales if the campaign has been in progress for 1.5 weeks.
If for bivariate data `bar x = 10, bar y = 12,` v(x) = 9, σy = 4 and r = 0.6 estimate y, when x = 5.
Identify the regression equations of x on y and y on x from the following equations, 2x + 3y = 6 and 5x + 7y − 12 = 0
If for a bivariate data byx = – 1.2 and bxy = – 0.3 then find r.
The equations of the two lines of regression are 3x + 2y − 26 = 0 and 6x + y − 31 = 0 Find
- Means of X and Y
- Correlation coefficient between X and Y
- Estimate of Y for X = 2
- var (X) if var (Y) = 36
Find the equation of the line of regression of Y on X for the following data:
n = 8, `sum(x_i - barx).(y_i - bary) = 120, barx = 20, bary = 36, sigma_x = 2, sigma_y = 3`
Regression equation of X on Y is_________
Choose the correct alternative:
The slope of the line of regression of y on x is called the ______
Choose the correct alternative:
If the lines of regression of Y on X is y = `x/4` and X on Y is x = `y/9 + 1` then the value of r is
Choose the correct alternative:
u = `(x - 20)/5` and v = `(y - 30)/4`, then bxy =
Choose the correct alternative:
y = 5 – 2.8x and x = 3 – 0.5 y be the regression lines, then the value of byx is
State whether the following statement is True or False:
The equations of two regression lines are 10x – 4y = 80 and 10y – 9x = 40. Then bxy = 0.9
State whether the following statement is True or False:
y = 5 + 2.8x and x = 3 + 0.5y be the regression lines of y on x and x on y respectively, then byx = – 0.5
State whether the following statement is True or False:
If equation of regression lines are 3x + 2y – 26 = 0 and 6x + y – 31= 0, then mean of X is 7
State whether the following statement is True or False:
bxy is the slope of regression line of y on x
The equations of the two lines of regression are 2x + 3y − 6 = 0 and 5x + 7y − 12 = 0. Identify the regression lines
The age in years of 7 young couples is given below. Calculate husband’s age when wife’s age is 38 years.
| Husband (x) | 21 | 25 | 26 | 24 | 22 | 30 | 20 |
| Wife (y) | 19 | 20 | 24 | 20 | 22 | 24 | 18 |
The equations of the two lines of regression are 6x + y − 31 = 0 and 3x + 2y – 26 = 0. Identify the regression lines
Two samples from bivariate populations have 15 observations each. The sample means of X and Y are 25 and 18 respectively. The corresponding sum of squares of deviations from means are 136 and 148 respectively. The sum of product of deviations from respective means is 122. Obtain the regression equation of x on y
If n = 5, Σx = Σy = 20, Σx2 = Σy2 = 90, Σxy = 76 Find the regression equation of x on y
If n = 6, Σx = 36, Σy = 60, Σxy = –67, Σx2 = 50, Σy2 =106, Estimate y when x is 13
The regression equation of x on y is 40x – 18y = 214 ......(i)
The regression equation of y on x is 8x – 10y + 66 = 0 ......(ii)
Solving equations (i) and (ii),
`barx = square`
`bary = square`
∴ byx = `square/square`
∴ bxy = `square/square`
∴ r = `square`
Given variance of x = 9
∴ byx = `square/square`
∴ `sigma_y = square`
If `(x - 1)/l = (y - 2)/m = (z + 1)/n` is the equation of the line through (1, 2, -1) and (-1, 0, 1), then (l, m, n) is ______
If `bar"X"` = 40, `bar"Y"` = 6, σx = 10, σy = 1.5 and r = 0.9 for the two sets of data X and Y, then the regression line of X on Y will be:
For certain bivariate data on 5 pairs of observations given:
∑x = 20, ∑y = 20, ∑x2 = 90, ∑y2 = 90, ∑xy = 76 then bxy = ______.
The management of a large furniture store would like to determine sales (in thousands of ₹) (X) on a given day on the basis of number of people (Y) that visited the store on that day. The necessary records were kept, and a random sample of ten days was selected for the study. The summary results were as follows:
`sumx_i = 370 , sumy_i = 580, sumx_i^2 = 17200 , sumy_i^2 = 41640, sumx_iy_i = 11500, n = 10`
For a bivariate data `barx = 10`, `bary = 12`, V(X) = 9, σy = 4 and r = 0.6
Estimate y when x = 5
Solution: Line of regression of Y on X is
`"Y" - bary = square ("X" - barx)`
∴ Y − 12 = `r.(σ_y)/(σ_x)("X" - 10)`
∴ Y − 12 = `0.6 xx 4/square ("X" - 10)`
∴ When x = 5
Y − 12 = `square(5 - 10)`
∴ Y − 12 = −4
∴ Y = `square`
