Advertisements
Advertisements
प्रश्न
Find the value of discriminant.
`sqrt2x^2 + 4x + 2sqrt2 = 0`
उत्तर
`sqrt2x^2 + 4x + 2sqrt2 = 0`
Comparing the given equation with ax2 + bx + c = 0, we get,
`a = sqrt2, b = 4, c = 2sqrt2`
So, the discriminant (D),
`∴ b^2 − 4ac = (4)^2 − 4 × (sqrt2) × (2sqrt2)`
`∴ b^2 − 4ac = 16 − 16`
`∴ b^2 − 4ac = 0`.
APPEARS IN
संबंधित प्रश्न
Find the roots of the quadratic equation 2x2 + x + 4 = 0
The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/h more than that of the passenger train, find the average speed of the two trains.
`3x^2-2x-1=0`
`5x^2-6x-2=0`
`4x^2+4bx-(a^2-b^2)=0`
The sum of the areas of two squares is `640m^2` . If the difference in their perimeter be 64m, find the sides of the two square
The area of right -angled triangle is 165 sq meters. Determine its base and altitude if the latter exceeds the former by 7 meters.
The hypotenuse of a right=-angled triangle is 20 meters. If the difference between the lengths of the other sides be 4 meters, find the other sides
The ratio of the sum and product of the roots of the equation `7x^2-12x+18=0` is
(a) 7:12 (b)7:18 (c)3:2 (d)2:3
Sum of the areas of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of the two squares ?
Solve the following quadratic equation by completing the square method.
9y2 – 12y + 2 = 0
Fill in the gaps and complete.
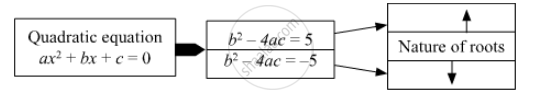
Fill in the gap and complete.

Determine the nature of roots of the following quadratic equation.
2y2 – 7y + 2 = 0
The difference of two natural numbers is 3 and the difference of their reciprocals is \[\frac{3}{28}\].Find the numbers.
The value of \[\sqrt{6 + \sqrt{6 + \sqrt{6 +}}} . . . .\] is
Complete the following activity to solve the given word problem. The Sum of squares of two consecutive even natural numbers is 244, then find those numbers.
Activity: Let the first even natural number be x
Therefore its consecutive even natural number will be = (______)
By the given condition,
x2 + (x + 2)2 = 244
x2 + x2 + 4x + 4 – (______) = 0
2x2 + 4x – 240 = 0
x2 + 2x – 120 = 0
x2 + (______) – (______) – 120 = 0
x(x + 12) – (______) (x + 12) = 0
(x + 12)(x – 10) = 0
x = (______)/x = 10
But natural number cannot be negative, x = – 12 is not possible.
Therefore first even natural number is x = 10.
Second even consecutive natural number = x + 2 = 10 + 2 = 12.
If a, b, care in continued proportion, then show that `(a + b)^2/(ab) = (b + c)^2/(bc)`.
Since a, b, c are in continued proportion
∴ `a/b = square/square` = k(say)
⇒ b = `square`, a = `square` = `square`.k = `square`.k2
Now, L.H.S. = `(a + b)^2/(a.square) = (square + square)^2/(square*square)`
= `(squarek^2(k + 1)^2)/(square*square)`
= `(k + 1)^2/square`
R.H.S. = `(b + c)^2/(b.square) = (square + square)^2/(square*square) = (square (k + 1)^2)/(square*square)`
= `(k + 1)^2/square`
L.H.S. = `square`
Had Aarush scored 8 more marks in a Mathematics test, out of 35 marks, 7 times these marks would have been 4 less than square of his actual marks. How many marks did he get in the test?
