Advertisements
Advertisements
प्रश्न
In ΔABC, the mid-points of AB, BC and AC are P, Q and R respectively. Prove that BQRP is a parallelogram and that its area is half of ΔABC.
उत्तर
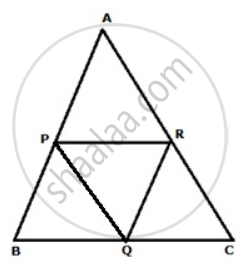
Since P and R are mid-points of AB and AC respectively.
Therefore, PR || BC and PR = `(1)/(2)"BC"` ...........(i)
Also Q is mid-point of BC,
⇒ QC = `(1)/(2)"BC"` ...........(ii)
From (i) and (ii)
PR || BC and PR = QC
⇒ PR || QC and PR = QC ..........(iii)
Similarly Q and R are mid-point of BC and AC respectively
Therefore, QR || BP and QR = BP ..........(iv)
⇒ PQ is a digonal of ||gm BQRP
ar(ΔPQR) = ar(ΔBQP) ....(v) (diagonal of a ||gm divides it into two triangles of equal areas)
Similarly QCRP and QRAP are || gm and
ar(ΔPQR) = ar(ΔQCR) = ar(ΔAPR) ..........(vi)
From (v) and (vi)
ar(ΔPQR) = ar(ΔBQP) = ar(ΔQCR) = ar(ΔAPR)
Now,
ar(ΔABC) = ar(ΔPQR) + ar(ΔBQP) + ar(ΔQCR) + ar(ΔAPR)
⇒ ar(ΔABC) = 4ar(ΔPQR)
⇒ ar(ΔPQR) = `(1)/(4)"ar(ΔABC)"` ..........(vii)
ar(||gm BQRP) = ar(ΔPQR) + ar(ΔBQP)
⇒ ar(||gm BQRP) = ar(ΔPQR) + ar(ΔPQR) ...(from(v))
⇒ ar(||gm BQRP) = 2ar(ΔPQR)
⇒ ar(||gm BQRP) = `2 xx (1)/(4)"ar(ΔABC)"` ...(from(vii))
⇒ ar(||gm BQRP) = `(1)/(2)"ar(ΔABC)"`.
APPEARS IN
संबंधित प्रश्न
ABCD is a parallelogram. P and T are points on AB and DC respectively and AP = CT. Prove that PT and BD bisect each other.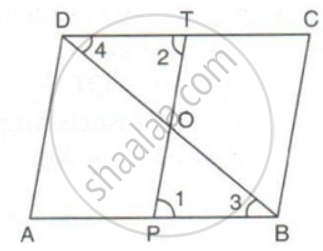
ABCD is a quadrilateral P, Q, R and S are the mid-points of AB, BC, CD and AD. Prove that PQRS is a parallelogram.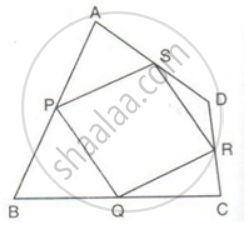
Prove that the line segment joining the mid-points of the diagonals of a trapezium is parallel to each of the parallel sides, and is equal to half the difference of these sides.
In a parallelogram PQRS, M and N are the midpoints of the opposite sides PQ and RS respectively. Prove that
RN and RM trisect QS.
ABCD is a trapezium in which side AB is parallel to side DC. P is the mid-point of side AD. IF Q is a point on the Side BC such that the segment PQ is parallel to DC, prove that PQ = `(1)/(2)("AB" + "DC")`.
In the given figure, PQRS is a parallelogram in which PA = AB = Prove that: SA ‖ QB and SA = QB.
Prove that the diagonals of a kite intersect each other at right angles.
PQRS is a parallelogram and O is any point in its interior. Prove that: area(ΔPOQ) + area(ΔROS) - area(ΔQOR) + area(ΔSOP) = `(1)/(2)`area(|| gm PQRS)
In ΔPQR, PS is a median. T is the mid-point of SR and M is the mid-point of PT. Prove that: ΔPMR = `(1)/(8)Δ"PQR"`.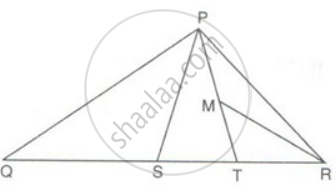
The medians QM and RN of ΔPQR intersect at O. Prove that: area of ΔROQ = area of quadrilateral PMON.
