Advertisements
Advertisements
प्रश्न
In problems 1 – 6, using the table estimate the value of the limit.
`lim_(x -> 2) (x - 2)/(x^2 - x - 2)`
| x | 1.9 | 1.99 | 1.999 | 2.001 | 2.01 | 2.1 |
| f(x) | 0.344820 | 0.33444 | 0.33344 | 0.333222 | 0.33222 | 0.332258 |
उत्तर
`lim_(x -> 2) (x - 2)/(x^2 - x - 2) = lim_(x -> 2) ( x - 2)/((x - 2)(x + 1))`
= `lim_(x -> 2) (x - 2)/(x + 1)`
| x | 1.9 | 1.99 | 1.999 | 2.001 | 20.1 | 2.1 |
| f(x) |
`1/(1.9 + 1)` = `1/2.9` = 0.34 |
`1/(1.99 + 1)` = `1/2.99` = 0.33 |
`1/(1.999 + 1)` = `1/2.99` = 0.33 |
`1/(2.001 + 1)` = `1/3.001` = 0.33 |
`1/(2.01 + 1)` = `1/3.01` = 0.33 |
`1/(2.1 + 1)` = `1/3.1` = 0.32 |
`lim_(x -> 2) (x - 2)/(x^2 - x - 2)` = 0.3
APPEARS IN
संबंधित प्रश्न
Evaluate the following limit:
`lim_(y -> -3) [(y^5 + 243)/(y^3 + 27)]`
Evaluate the following limit :
`lim_(x -> 7)[((root(3)(x) - root(3)(7))(root(3)(x) + root(3)(7)))/(x - 7)]`
Evaluate the following limit :
`lim_(x -> 0)[((1 - x)^8 - 1)/((1 - x)^2 - 1)]`
Evaluate the following limit :
`lim_(y -> 1)[(2y - 2)/(root(3)(7 + y) - 2)]`
In the following example, given ∈ > 0, find a δ > 0 such that whenever, |x – a| < δ, we must have |f(x) – l| < ∈.
`lim_(x -> 2)(2x + 3)` = 7
Evaluate the following :
`lim_(x -> 1) [(x + 3x^2 + 5x^3 + ... + (2"n" - 1)x^"n" - "n"^2)/(x - 1)]`
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 3) (4 - x)`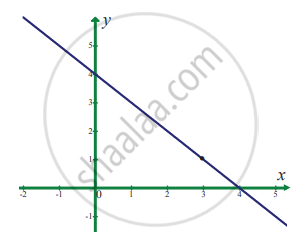
If the limit of f(x) as x approaches 2 is 4, can you conclude anything about f(2)? Explain reasoning
Verify the existence of `lim_(x -> 1) f(x)`, where `f(x) = {{:((|x - 1|)/(x - 1)",", "for" x ≠ 1),(0",", "for" x = 1):}`
Evaluate the following limits:
`lim_(x -> 2) (1/x - 1/2)/(x - 2)`
Evaluate the following limits:
`lim_(x -> oo) (1 + x - 3x^3)/(1 + x^2 +3x^3)`
Show that `lim_("n" -> oo) 1/1.2 + 1/2.3 + 1/3.4 + ... + 1/("n"("n" + 1))` = 1
Evaluate the following limits:
`lim_(alpha -> 0) (sin(alpha^"n"))/(sin alpha)^"m"`
Evaluate the following limits:
`lim_(x -> pi) (1 + sinx)^(2"cosec"x)`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(1 + sinx) - sqrt(1 - sinx))/tanx`
Evaluate the following limits:
`lim_(x -> 0) ("e"^("a"x) - "e"^("b"x))/x`
Choose the correct alternative:
`lim_(x -> 0) ("e"^tanx - "e"^x)/(tan x - x)` =
`lim_(x -> 0) ((2 + x)^5 - 2)/((2 + x)^3 - 2)` = ______.
If `lim_(x -> 1) (x + x^2 + x^3|+ .... + x^n - n)/(x - 1)` = 820, (n ∈ N) then the value of n is equal to ______.
