Advertisements
Advertisements
प्रश्न
Kiran plays a game of throwing a fair die 3 times but to quit as and when she gets a six. Kiran gets +1 point for a six and –1 for any other number.
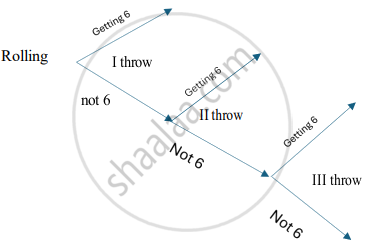
- If X denotes the random variable “points earned” then what are the possible values X can take?
- Find the probability distribution of this random variable X.
- Find the expected value of the points she gets.
उत्तर
i. X = −3, −1, 0, 1
ii. P(X = −3) = `5/6 xx 5/6 xx 5/6 = 125/216`
P(X = −1) = `5/6 xx 5/6 xx 1/6 = 25/216`
P(X = 0) = `5/6 xx 1/6 = 5/36`
P(X = 1) = `1/6`
Required probability distribution:
| X | −3 | −1 | 0 | 1 |
| P(X) | `125/216` | `25/216` | `5/36` | `1/6` |
iii. Expected value = `sumpx`
= `(−3)(125/216) + (-1)(25/216) + 0 + (1/6)`
= `-91/54`
= `-1 37/54 ≈ -1.69`
APPEARS IN
संबंधित प्रश्न
Probability distribution of X is given by
| X = x | 1 | 2 | 3 | 4 |
| P(X = x) | 0.1 | 0.3 | 0.4 | 0.2 |
Find P(X ≥ 2) and obtain cumulative distribution function of X
An urn contains 25 balls of which 10 balls bear a mark ‘X’ and the remaining 15 bear a mark ‘Y’. A ball is drawn at random from the urn, its mark is noted down and it is replaced. If 6 balls are drawn in this way, find the probability that
(i) all will bear ‘X’ mark.
(ii) not more than 2 will bear ‘Y’ mark.
(iii) at least one ball will bear ‘Y’ mark
(iv) the number of balls with ‘X’ mark and ‘Y’ mark will be equal.
There are 4 cards numbered 1 to 4, one number on one card. Two cards are drawn at random without replacement. Let X denote the sum of the numbers on the two drawn cards. Find the mean and variance of X.
A random variable X has the following probability distribution:
| Values of X : | −2 | −1 | 0 | 1 | 2 | 3 |
| P (X) : | 0.1 | k | 0.2 | 2k | 0.3 | k |
Find the value of k.
Two cards are drawn from a well shuffled pack of 52 cards. Find the probability distribution of the number of aces.
Find the probability distribution of the number of heads, when three coins are tossed.
Find the mean and standard deviation of each of the following probability distribution :
| xi: | 0 | 1 | 3 | 5 |
| pi : | 0.2 | 0.5 | 0.2 | 0.1 |
Find the mean and standard deviation of each of the following probability distribution :
| xi : | -3 | -1 | 0 | 1 | 3 |
| pi : | 0.05 | 0.45 | 0.20 | 0.25 | 0.05 |
A die is tossed twice. A 'success' is getting an odd number on a toss. Find the variance of the number of successes.
Three cards are drawn at random (without replacement) from a well shuffled pack of 52 cards. Find the probability distribution of number of red cards. Hence, find the mean of the distribution .
A random variable X takes the values 0, 1, 2, 3 and its mean is 1.3. If P (X = 3) = 2 P (X = 1) and P (X = 2) = 0.3, then P (X = 0) is
Three fair coins are tossed simultaneously. If X denotes the number of heads, find the probability distribution of X.
For the following probability density function (p. d. f) of X, find P(X < 1) and P(|x| < 1)
`f(x) = x^2/18, -3 < x < 3`
= 0, otherwise
If the demand function is D = 150 - p2 - 3p, find marginal revenue, average revenue and elasticity of demand for price p = 3.
Verify the following function, which can be regarded as p.m.f. for the given values of X :
| X = x | -1 | 0 | 1 |
| P(x) | -0.2 | 1 | 0.2 |
Find mean and standard deviation of the continuous random variable X whose p.d.f. is given by f(x) = 6x(1 - x);= (0); 0 < x < 1(otherwise)
A fair coin is tossed 12 times. Find the probability of getting exactly 7 heads .
If random variable X has probability distribution function.
f(x) = `c/x`, 1 < x < 3, c > 0, find c, E(x) and Var(X)
If p : It is a day time , q : It is warm
Give the verbal statements for the following symbolic statements :
(a) p ∧ ∼ q (b) p v q (c) p ↔ q
If X ∼ N (4,25), then find P(x ≤ 4)
Solve the following:
Identify the random variable as either discrete or continuous in each of the following. Write down the range of it.
A highway safety group is interested in studying the speed (km/hrs) of a car at a check point.
A random variable X has the following probability distribution :
| x = x | 0 | 1 | 2 | 3 | 7 | |||
| P(X=x) | 0 | k | 2k | 2k | 3k | k2 | 2k2 | 7k2 + k |
Determine (i) k
(ii) P(X> 6)
(iii) P(0<X<3).
Determine whether each of the following is a probability distribution. Give reasons for your answer.
| x | 0 | 1 | 2 | 3 | 4 |
| P(x) | 0.1 | 0.5 | 0.2 | –0.1 | 0.3 |
A die is thrown 4 times. If ‘getting an odd number’ is a success, find the probability of at most 2 successes.
10 balls are marked with digits 0 to 9. If four balls are selected with replacement. What is the probability that none is marked 0?
State whether the following is True or False :
If r.v. X assumes the values 1, 2, 3, ……. 9 with equal probabilities, E(x) = 5.
Solve the following problem :
The probability that a lamp in the classroom will burn is 0.3. 3 lamps are fitted in the classroom. The classroom is unusable if the number of lamps burning in it is less than 2. Find the probability that the classroom cannot be used on a random occasion.
Solve the following problem :
In a large school, 80% of the students like mathematics. A visitor asks each of 4 students, selected at random, whether they like mathematics.
Find the probability that the visitor obtains the answer yes from at least 3 students.
The probability distribution of a random variable x is given as under:
P(X = x) = `{{:("k"x^2, "for" x = 1"," 2"," 3),(2"k"x, "for" x = 4"," 5"," 6),(0, "otherwise"):}`
where k is a constant. Calculate E(3X2)
If the p.m.f of a r. v. X is
P(x) = `c/x^3`, for x = 1, 2, 3
= 0, otherwise
then E(X) = ______.
