Advertisements
Advertisements
प्रश्न
For the following probability density function (p. d. f) of X, find P(X < 1) and P(|x| < 1)
`f(x) = x^2/18, -3 < x < 3`
= 0, otherwise
उत्तर
We have
P(X < 1) = `int_-3^1 f(x) dx`
= `int_-3^1 x^2/18dx`
= `[x^3/54]_-3^1`
= `1/54 - ((-27)/54)`
= `28/54`
= `14/27`
= 0.5185
Now |X| < 1
`\implies` ± X < 1
∴ X < 1, – X < 1,
i.e. X > – 1
i.e. – 1 < X < 1
∴ Required Probability = `int_-1^1 f(x)dx`
= `int_-1^1 x^2/18dx`
= `[x^3/54]_-1^1`
= `1/54 + 1/54`
= `2/54`
= `1/27`
= 0.03704
APPEARS IN
संबंधित प्रश्न
From a lot of 25 bulbs of which 5 are defective a sample of 5 bulbs was drawn at random with replacement. Find the probability that the sample will contain -
(a) exactly 1 defective bulb.
(b) at least 1 defective bulb.
State the following are not the probability distributions of a random variable. Give reasons for your answer.
| X | 0 | 1 | 2 | 3 | 4 |
| P(X) | 0.1 | 0.5 | 0.2 | -0.1 | 0.3 |
State the following are not the probability distributions of a random variable. Give reasons for your answer.
| Z | 3 | 2 | 1 | 0 | -1 |
| P(Z) | 0.3 | 0.2 | 0.4 | 0.1 | 0.05 |
An urn contains 5 red and 2 black balls. Two balls are randomly drawn. Let X represents the number of black balls. What are the possible values of X? Is X a random variable?
Find the probability distribution of number of heads in two tosses of a coin.
Find the probability distribution of number of tails in the simultaneous tosses of three coins.
Find the probability distribution of the number of successes in two tosses of a die, where a success is defined as
(i) number greater than 4
(ii) six appears on at least one die
A coin is biased so that the head is 3 times as likely to occur as tail. If the coin is tossed twice, find the probability distribution of number of tails.
The random variable X has probability distribution P(X) of the following form, where k is some number:
`P(X = x) {(k, if x = 0),(2k, if x = 1),(3k, if x = 2),(0, "otherwise"):}`
- Determine the value of 'k'.
- Find P(X < 2), P(X ≥ 2), P(X ≤ 2).
Two dice are thrown simultaneously. If X denotes the number of sixes, find the expectation of X.
There are 4 cards numbered 1, 3, 5 and 7, one number on one card. Two cards are drawn at random without replacement. Let X denote the sum of the numbers on the two drawn cards. Find the mean 'and variance of X.
Two numbers are selected at random (without replacement) from the first five positive integers. Let X denote the larger of the two numbers obtained. Find the mean and variance of X
Three persons A, B and C shoot to hit a target. If A hits the target four times in five trials, B hits it three times in four trials and C hits it two times in three trials, find the probability that:
1) Exactly two persons hit the target.
2) At least two persons hit the target.
3) None hit the target.
Let, X denote the number of colleges where you will apply after your results and P(X = x) denotes your probability of getting admission in x number of colleges. It is given that
where k is a positive constant. Find the value of k. Also find the probability that you will get admission in (i) exactly one college (ii) at most 2 colleges (iii) at least 2 colleges.
A class has 15 students whose ages are 14, 17, 15, 14, 21, 19, 20, 16, 18, 17, 20, 17, 16, 19 and 20 years respectively. One student is selected in such a manner that each has the same chance of being selected and the age X of the selected student is recorded. What is the probability distribution of the random variable X?
Five defective bolts are accidently mixed with twenty good ones. If four bolts are drawn at random from this lot, find the probability distribution of the number of defective bolts.
Find the probability distribution of the number of white balls drawn in a random draw of 3 balls without replacement, from a bag containing 4 white and 6 red balls
Find the probability distribution of Y in two throws of two dice, where Y represents the number of times a total of 9 appears.
A fair die is tossed twice. If the number appearing on the top is less than 3, it is a success. Find the probability distribution of number of successes.
Let X represent the difference between the number of heads and the number of tails when a coin is tossed 6 times. What are the possible values of X?
Four balls are to be drawn without replacement from a box containing 8 red and 4 white balls. If X denotes the number of red balls drawn, then find the probability distribution of X.
The probability distribution of a random variable X is given below:
| x | 0 | 1 | 2 | 3 |
| P(X) | k |
\[\frac{k}{2}\]
|
\[\frac{k}{4}\]
|
\[\frac{k}{8}\]
|
Determine the value of k .
The probability distribution of a random variable X is given below:
| x | 0 | 1 | 2 | 3 |
| P(X) | k |
\[\frac{k}{2}\]
|
\[\frac{k}{4}\]
|
\[\frac{k}{8}\]
|
Determine P(X ≤ 2) and P(X > 2) .
Find the mean and standard deviation of each of the following probability distribution :
| xi: | 0 | 1 | 3 | 5 |
| pi : | 0.2 | 0.5 | 0.2 | 0.1 |
Two cards are drawn simultaneously from a pack of 52 cards. Compute the mean and standard deviation of the number of kings.
Two bad eggs are accidently mixed up with ten good ones. Three eggs are drawn at random with replacement from this lot. Compute the mean for the number of bad eggs drawn.
A pair of fair dice is thrown. Let X be the random variable which denotes the minimum of the two numbers which appear. Find the probability distribution, mean and variance of X.
A fair die is tossed. Let X denote twice the number appearing. Find the probability distribution, mean and variance of X.
A fair coin is tossed four times. Let X denote the longest string of heads occurring. Find the probability distribution, mean and variance of X.
In roulette, Figure, the wheel has 13 numbers 0, 1, 2, ...., 12 marked on equally spaced slots. A player sets Rs 10 on a given number. He receives Rs 100 from the organiser of the game if the ball comes to rest in this slot; otherwise he gets nothing. If X denotes the player's net gain/loss, find E (X).
If X denotes the number on the upper face of a cubical die when it is thrown, find the mean of X.
If the probability distribution of a random variable X is as given below:
Write the value of P (X ≤ 2).
| X = xi : | 1 | 2 | 3 | 4 |
| P (X = xi) : | c | 2c | 4c | 4c |
If a random variable X has the following probability distribution:
| X : | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| P (X) : | a | 3a | 5a | 7a | 9a | 11a | 13a | 15a | 17a |
then the value of a is
A random variable X takes the values 0, 1, 2, 3 and its mean is 1.3. If P (X = 3) = 2 P (X = 1) and P (X = 2) = 0.3, then P (X = 0) is
A random variable has the following probability distribution:
| X = xi : | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P (X = xi) : | 0 | 2 p | 2 p | 3 p | p2 | 2 p2 | 7 p2 | 2 p |
The value of p is
Mark the correct alternative in the following question:
For the following probability distribution:
| X: | −4 | −3 | −2 | −1 | 0 |
| P(X): | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 |
The value of E(X) is
A die is tossed twice. A 'success' is getting an even number on a toss. Find the variance of number of successes.
A random variable X has the following probability distribution :
| X = x | -2 | -1 | 0 | 1 | 2 | 3 |
| P(x) | 0.1 | k | 0.2 | 2k | 0.3 | k |
Find the value of k and calculate mean.
A fair coin is tossed 12 times. Find the probability of getting exactly 7 heads .
A fair coin is tossed 12 times. Find the probability of getting at least 2 heads .
If p : It is a day time , q : It is warm
Give the verbal statements for the following symbolic statements :
(a) p ∧ ∼ q (b) p v q (c) p ↔ q
From the following data, find the crude death rates (C.D.R.) for Town I and Town II, and comment on the results :
| Age Group (in years) | Town I | Town II | ||
| Population | No. of deaths | Population | No. of deaths | |
| 0-10 | 1500 | 45 | 6000 | 150 |
| 10-25 | 5000 | 30 | 6000 | 40 |
| 25 - 45 | 3000 | 15 | 5000 | 20 |
| 45 & above | 500 | 22 | 3000 | 54 |
A random variable X has the following probability distribution :
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| P(X) | C | 2C | 2C | 3C | C2 | 2C2 | 7C2+C |
Find the value of C and also calculate the mean of this distribution.
An urn contains 5 red and 2 black balls. Two balls are drawn at random. X denotes number of black balls drawn. What are possible values of X?
Determine whether each of the following is a probability distribution. Give reasons for your answer.
| x | 0 | 1 | 2 | 3 | 4 |
| P(x) | 0.1 | 0.5 | 0.2 | –0.1 | 0.3 |
Determine whether each of the following is a probability distribution. Give reasons for your answer.
| x | 0 | 1 | 2 |
| P(x) | 0.1 | 0.6 | 0.3 |
Determine whether each of the following is a probability distribution. Give reasons for your answer.
| x | 0 | 1 | 2 |
| P(x) | 0.3 | 0.4 | 0.2 |
A sample of 4 bulbs is drawn at random with replacement from a lot of 30 bulbs which includes 6 defective bulbs. Find the probability distribution of the number of defective bulbs.
A die is thrown 4 times. If ‘getting an odd number’ is a success, find the probability of 2 successes
A die is thrown 4 times. If ‘getting an odd number’ is a success, find the probability of at most 2 successes.
In a multiple choice test with three possible answers for each of the five questions, what is the probability of a candidate getting four or more correct answers by random choice?
Defects on plywood sheet occur at random with the average of one defect per 50 sq.ft. Find the probability that such a sheet has:
- no defect
- at least one defect
Use e−1 = 0.3678
Solve the following problem :
Find the probability of the number of successes in two tosses of a die, where success is defined as number greater than 4.
Solve the following problem :
If a fair coin is tossed 4 times, find the probability that it shows head in the first 2 tosses and tail in last 2 tosses.
Solve the following problem :
In a large school, 80% of the students like mathematics. A visitor asks each of 4 students, selected at random, whether they like mathematics.
Calculate the probabilities of obtaining an answer yes from all of the selected students.
Solve the following problem :
It is observed that it rains on 10 days out of 30 days. Find the probability that it rains on exactly 3 days of a week.
A random variable X has the following probability distribution
| X | 2 | 3 | 4 |
| P(x) | 0.3 | 0.4 | 0.3 |
Then the variance of this distribution is
Find the probability distribution of the number of doublets in three throws of a pair of dice
Find the mean and variance of the number randomly selected from 1 to 15
Two biased dice are thrown together. For the first die P(6) = `1/2`, the other scores being equally likely while for the second die, P(1) = `2/5` and the other scores are equally likely. Find the probability distribution of ‘the number of ones seen’.
The random variable X can take only the values 0, 1, 2. Given that P(X = 0) = P(X = 1) = p and that E(X2) = E[X], find the value of p
Let X be a discrete random variable whose probability distribution is defined as follows:
P(X = x) = `{{:("k"(x + 1), "for" x = 1"," 2"," 3"," 4),(2"k"x, "for" x = 5"," 6"," 7),(0, "Otherwise"):}`
where k is a constant. Calculate Standard deviation of X.
The probability distribution of a discrete random variable X is given as under:
| X | 1 | 2 | 4 | 2A | 3A | 5A |
| P(X) | `1/2` | `1/5` | `3/25` | `1/10` | `1/25` | `1/25` |
Calculate: Variance of X
The probability distribution of a random variable x is given as under:
P(X = x) = `{{:("k"x^2, "for" x = 1"," 2"," 3),(2"k"x, "for" x = 4"," 5"," 6),(0, "otherwise"):}`
where k is a constant. Calculate E(3X2)
For the following probability distribution:
| X | – 4 | – 3 | – 2 | – 1 | 0 |
| P(X) | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 |
E(X) is equal to ______.
A random variable x has to following probability distribution.
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P(x) | 0 | k | 2k | 2k | 3k | k2 | 2k2 | 7k2 + k |
Determine
If the p.m.f of a r. v. X is
P(x) = `c/x^3`, for x = 1, 2, 3
= 0, otherwise
then E(X) = ______.
Find the mean of number randomly selected from 1 to 15.
Two balls are drawn at random one by one with replacement from an urn containing equal number of red balls and green balls. Find the probability distribution of number of red balls. Also, find the mean of the random variable.
A box contains 30 fruits, out of which 10 are rotten. Two fruits are selected at random one by one without replacement from the box. Find the probability distribution of the number of unspoiled fruits. Also find the mean of the probability distribution.
Kiran plays a game of throwing a fair die 3 times but to quit as and when she gets a six. Kiran gets +1 point for a six and –1 for any other number.
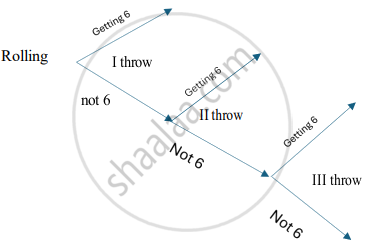
- If X denotes the random variable “points earned” then what are the possible values X can take?
- Find the probability distribution of this random variable X.
- Find the expected value of the points she gets.
