Advertisements
Advertisements
प्रश्न
किसी त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है। उस त्रिभुज ABC के लिए इस परिणाम का सत्यापन कीजिए जिसके शीर्ष A(4, -6), B(3, -2) और C(5, 2) हैं।
Advertisements
उत्तर
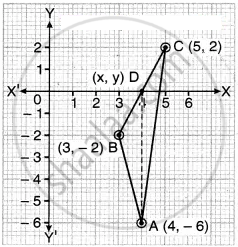
दिया है ∆ABC के शीर्षों A(4, -6), B(3, -2) और C(5, 2) हैं तथा माध्यिका AD है, जहाँ BC का मध्य-बिन्दु D(x, y) है तो
`x = (3 + 5)/2 = 8/2 = 0`
`y = (-2 + 2)/2 = 0/2 = 0`
अब ∆ADB में A (4, -6), D (4, 0) एवं B (3, -2)
ar (ADB) = `1/2` [4 (0 + 2) + 4 (-2 + 6) + 3 (-6 - 0)]
= `1/2` [4 (2) + 4 (4) + 3 (-6)]
= `1/2` [8 + 16 - 18]
= `1/2` (24 - 18)
= `1/2 xx 6`
= 3 वर्ग मात्रक
एवं ∆ADC में A(4, -6), D(4, 0) एवं C(5, 2) हैं
ar (ADC) = `1/2` [4 (0 - 2) + 4 (2 + 6) + 5 (-6 - 0)]
= `1/2` [4 (-2) + 4 (8) + 5 (-6)]
= `1/2` [-8 + 32 - 30]
= `1/2 xx [-6]`
= -3 वर्ग मात्रक
लेकिन क्षेत्रफल एक धनात्मक राशि होती है = ar (ADC) = 3 वर्ग मात्रक
ar (ADB) = ar (ADC)
अतः किसी त्रिभुज की एक माध्यिका उस त्रिभुज को दो बराबर क्षेत्रफलों वाले त्रिभुजों में विभाजित करती है।
इति सिद्धम्
संबंधित प्रश्न
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष हैं:
(2, 3), (-1, 0), (2, -4)
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष हैं:
(-5, -1), (3, -5), (5, 2)
शीर्षों (0, -1), (2, 1) और (0, 3) वाले त्रिभुज की भुजाओं के मध्य-बिंदुओं से बनने वाले त्रिभुज का क्षेत्रफल ज्ञात कीजिए। इस क्षेत्रफल का दिए हुए त्रिभुज के क्षेत्रफल के साथ अनुपात ज्ञात कीजिए।
कृष्णानगर के एक सेकेंडरी स्कूल के कक्षा X के विद्यार्थियों को उनके बागवानी क्रियाकलाप के लिए, एक आयताकार भूखंड दिया गया है। गुलमोहर की पौध (sapling) को परस्पर 1m की दूरी पर इस भूखंड की परिसीमा (boundary) पर लगाया जाता है। इस भूखंड के अंदर एक त्रिभुजाकार घास लगा हुआ लॉन (lawn) है, जैसाकि आकृति में दर्शाया गया है। विद्यार्थियों को भूखंड के शेष भाग में है फूलों के पौधे के बीज बोने हैं।
(i) A को मूलबिंदु मानते हए, त्रिभुज के शीषों के निर्देशांक ज्ञात कीजिए।
(ii) यदि मूलबिंदु C हो, तो ∆PQR के शीर्षों के निर्देशांक क्या होंगे?
साथ ही, उपरोक्त दोनों स्थितियों में, त्रिभुजों के क्षेत्रफल ज्ञात कीजिए। आप क्या देखते हैं?
बिंदु (0, 5), (0, –9) और (3, 6) संरेख हैं।
x-अक्ष पर स्थित बिंदु Q के निर्देशांक ज्ञात कीजिए, जो बिंदुओं A(–5, –2) और B(4, –2) के लंब समद्विभाजक पर भी स्थित है। बिंदुओं Q, A और B से बनने वाले त्रिभुज का प्रकार भी बताइए।
बिंदु A(2, 9), B(a, 5) और C(5, 5) एक त्रिभुज ABC के शीर्ष हैं, जिसका∠B समकोण है। a के मान ज्ञात कीजिए और फिर ΔABC का क्षेत्रफल ज्ञात कीजिए।
k के मान ज्ञात कीजिए, यदि बिंदु A(k + 1, 2k), B(3k, 2k + 3) और C(5k – 1, 5k) संरेख हैं।
एक समद्विबाहु समकोण त्रिभुज का क्षेत्रफल 8 cm2 है। इसके कर्ण की लंबाई है।
एक त्रिभुज का परिमाप 50 cm है। त्रिभुज की एक भुजा छोटी भुजा से 4 cm लंबी है तथा तीसरी भुजा छोटी भुजा के दुगुने से 6 cm कम है। त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
