Advertisements
Advertisements
प्रश्न
Prove that the points (2a, 4a), (2a, 6a) and `(2a + sqrt3a, 5a)` are the vertices of an equilateral triangle.
उत्तर
The distance d between two points `(x_1, y_1)` and `(x_2, y_2)` is given by the formula
`d = sqrt((x_1 + x_2)^2 + (y_1- y_2)^2)`
In an equilateral triangle all the sides have equal length.
Here the tree points are A(2a, 4a), B(2a, 6a) and `C(2a + asqrt3, 5a)`
Let us now find out the lengths of all the three sides of the given triangle.
`AB = sqrt((2a - 2a)^2 + (4a - 6a)^2)`
`= sqrt((0)^2 + (-2a)^2)`
`= sqrt((0)^2 + (-2a)^2)`
`= sqrt(0 + 4a^2)`
AB = 2a
`BC = sqrt((2a - 2a - asqrt3)^2 + (6a - 5a))`
`= sqrt((-asqrt3)^2 + (a)^2)`
`= sqrt(3a^2 + a^2)`
`= sqrt(4a^2)`
AC = 2a
Since all the three sides have equal lengths the triangle has to be an equilateral triangle.
APPEARS IN
संबंधित प्रश्न
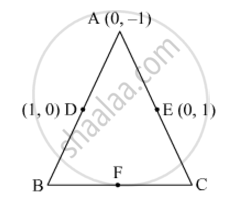
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
Prove that the area of a triangle with vertices (t, t −2), (t + 2, t + 2) and (t + 3, t) is independent of t.
The point A divides the join of P (−5, 1) and Q(3, 5) in the ratio k:1. Find the two values of k for which the area of ΔABC where B is (1, 5) and C(7, −2) is equal to 2 units.
Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
If A(5,2), B(2, -2) and C(-2, t) are the vertices of a right triangle with ∠B=90° , then find the value of t .
A(7, -3), B(5,3) and C(3,-1) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.
Using integration, find the area of triangle ABC, whose vertices are A(2, 5), B(4, 7) and C(6, 2).
Points A(–6, 10), B(–4, 6) and C(3, –8) are collinear such that AB = `2/9` AC.
Triangles having the same base have equal area.
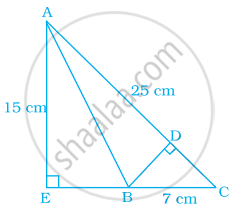
In the given figure, triangle AEC is right-angled at E, B is a point on EC, BD is the altitude of triangle ABC, AC = 25 cm, BC = 7 cm and AE = 15 cm. Find the area of triangle ABC and the length of DB.