Advertisements
Advertisements
प्रश्न
Show that the points A(1, 2), B(– 1, – 16) and C(0, – 7) lie on the graph of the linear equation y = 9x – 7.
उत्तर
Firstly, to draw the graph of equation y = 9x – 7
When x = 2, then y = 9 × 2 – 7
= 18 – 7
= 11
When x = – 2, then y = 9 × – 2 – 7
= – 18 – 7
= – 25
| x | 2 | – 2 |
| y | 11 | – 25 |
Here, we find two points D(2, 11) and E(–2, – 25).
So, draw the graph by plotting the points and joining the line DE.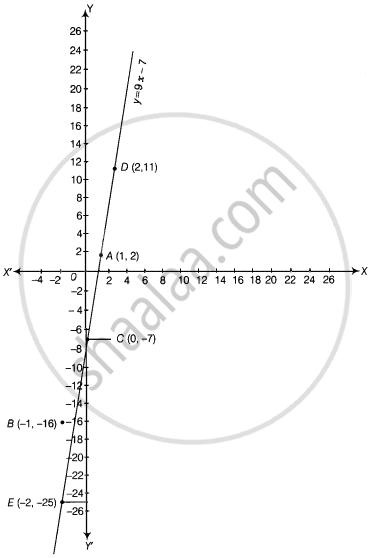
Now, we plot the given points A(1, 2), B(–1, –16) and C(0, –7) on the graph paper. We see that all the points lie on DE line.
APPEARS IN
संबंधित प्रश्न
If the point (3, 4) lies on the graph of the equation 3y = ax + 7, find the value of a.
If the point (2, -2) lies on the graph of the linear equation 5x + ky = 4, find the value of k.
Draw the graph for the equation, given below :
y = 7
Draw the graph of the equation 2x - 3y - 5 = 0
From the graph, find:
(i) x1, the value of x, when y = 7
(ii) x2, the value of x, when y = - 5.
Solve, graphically, the following pairs of equations :
`(x + 1)/(4) = (2)/(3)(1 - 2y)`
`(2 + 5y)/(3) = x/(7) -2`
By drawing a graph for each of the equations 3x + y + 5 = 0; 3y - x = 5 and 2x + 5y = 1 on the same graph paper; show that the lines given by these equations are concurrent (i.e. they pass through the same point). Take 2 cm = 1 unit on both the axes.
A pair of linear equations has no solution then the graphical representation is
Find the values.
y = 3x + 1
| x | − 1 | 0 | 1 | 2 |
| y |
The graph of the linear equation x + 2y = 7 passes through the point (0, 7).
Every point on the graph of a linear equation in two variables does not represent a solution of the linear equation.
