Advertisements
Advertisements
प्रश्न
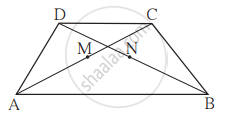
संलग्न आकृति में `square` ABCD यह समलंब चतुर्भुज है। AB || DC, बिंदु M तथा बिंदु N क्रमशः विकर्ण AC तथा विकर्ण DB के मध्यबिंदु है तो सिद्ध कीजिए कि MN || AB
उत्तर
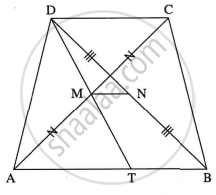
दत्त: `square` ABCD एक समलंब है।AB || DC
बिंदु M और N क्रमशः विकर्ण AC और DB के मध्यबिंदु हैं।
साध्य: MN || AB
रचना: रेख DM खींचो जो भुजा AB को बिंदु T पर प्रतिच्छेदित करे।
उपपत्ति:
भुजा DC || भुजा AB ...(दत्त)
तथा रेख AC एक तिर्यक रेखा है।
∴ ∠DAC ≅ ∠BAC ...(एकांतर कोण)
∴ ∠DCM ≅ ∠TAM ...(i) ...(A-M-C तथा A-T-B)
∆DCM तथा ∆TAM में,
∠DCM ≅ ∠TAM ...[(i) से]
रेख MC ≅ रेख MA ...(बिंदु M रेख AC का मध्यबिंदु है।)
∠DCM ≅ ∠TAM ...(शीर्षाभिमुख कोण)
∴ ∆DCM ≅ ∆TAM ...(सर्वांगसमता की को-भु-को कसौटी)
रेख DM ≅ रेख MT ...(स.त्रि.सं.भु) ...(ii)
∆DTB में,
बिंदु N, रेख DB का मध्यबिंदु है। ...(दत्त)
बिंदु M, रेख DT का मध्यबिंदु है। ...[(ii) से]
∴ रेख MN || भुजा TB ...(मध्यबिंदु प्रमेय)
∴ रेख MN || रेख AB ...(A-T-B)
APPEARS IN
संबंधित प्रश्न
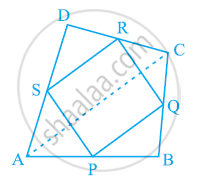
ABCD एक चतुर्भुज है जिसमें P, Q, R और S क्रमश: भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं (देखिए आकृति में)। AC उसका एक विकर्ण है। दर्शाइए कि
- SR || AC और SR = `1/2 AC` है।
- PQ = SR है।
- PQRS एक समांतर चतुर्भुज है।
ABCD एक समचतुर्भुज है और P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु है। दर्शाइए कि चतुर्भुज PQRS एक आयत है।
ABCD एक आयत है, जिसमें P, Q, R और S क्रमश: भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं। दर्शाइए कि चतुर्भुज PQRS एक समचतुर्भुज है।
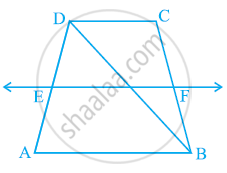
ABCD एक समलंब है, जिसमें AB || DC है। साथ ही, BD एक विकर्ण है और E भुजा AD का मध्य-बिंदु है। E से होकर एक रेखा AB के समांतर खींची गई है, जो BC को F पर प्रतिच्छेद करती है (देखिए आकृति में)। दर्शाइए कि F भुजा BC का मध्य-बिंदु है।
ABC एक त्रिभुज है जिसका कोण C समकोण है। कर्ण AB के मध्य-बिंदु M से होकर BC के समांतर खींची गई रेखा AC को D पर प्रतिच्छेद करती है। दर्शाइए कि
- D भुजा AC का मध्य-बिंदु है।
- MD ⊥ AC है।
- CM = MA = `1/2 AB` है।
D, E और F क्रमश: एक समबाहु त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिंदु हैं। दर्शाइए कि ∆DEF भी एक समबाहु त्रिभुज है।
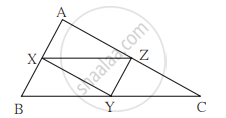
आकृति में ΔABC मे बिंदु X, Y, Z यह क्रमशः भुजाओं AB, BC तथा AC के मध्यबिंदु है। AB = 5 सेमी, AC = 9 सेमी तथा BC = 11 सेमी, तो XY, YZ, XZ की लंबाई ज्ञात कीजिए।
आकृति में `square` PQRS तथा `square` MNRL आयत है। बिंदु M यह PR का मध्यबिंदु है। तो सिद्ध कीजिए कि
(i) SL = LR, (ii) LN = `1/2` SQ

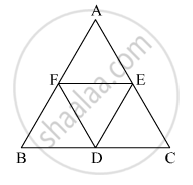
आकृति में ΔABC समबाहु त्रिभुज है जिसमें बिंदु F, D, E यह क्रमशः भुजा AB, भुजा BC, भुजा AC के मध्यबिंदु हैं तो सिद्ध कीजिए कि ΔFED यह समबाहु त्रिभुज है।
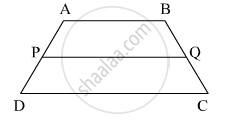
संलग्न आकृति में `square` ABCD समलंब चतुर्भुज है। AB || DC है। रेख AD तथा रेख BC के मध्यबिंदु क्रमशः P तथा Q हैं, तो सिद्ध कीजिए कि PQ || AB तथा PQ = `1/2` (AB + DC)