Advertisements
Advertisements
प्रश्न
Solve the following problem.
A ball of mass 100 g dropped on the ground from 5 m bounces repeatedly. During every bounce, 64% of the potential energy is converted into kinetic energy. Calculate the following:
- Coefficient of restitution.
- The speed with which the ball comes up from the ground after the third bounce.
- The impulse was given by the ball to the ground during this bounce.
- Average force exerted by the ground if this impact lasts for 250 ms.
- The average pressure exerted by the ball on the ground during this impact if the contact area of the ball is 0.5 cm2.
उत्तर
Given that, for every bounce, 64% of the initial energy is converted to final energy.
a) Coefficient of restitution in case of inelastic collision is given by,
e = `- "v"_"s"/"u"_"a" = - "v"/"u"` ....(1)
∴ `"e"^2 = "v"^2/"u"^2`
∴ v2 = e2 × u2
∴ `1/2 "mv"^2 = "e"^2 xx 1/2 "mu"^2`
∴ (K.E.)f = e2 × `1/2` mu2
∴ `("K.E.")_"f"/("K.E.")_"i" = "e"^2`
∴ `64/100 = "e"^2`
∴ e = 0.8
b) From equation (1),
v = – eu
∴ After first bounce,
v1 = - eu
after second bounce,
v2 = - ev1 = - e(- eu) = e2u
and after third bounce,
v3 = - ev2 = - e(- e2u) = - e3u
But u = `sqrt(2"gh")`
∴ `"v"_3 = - "e"^3 xx sqrt(2"gh") = -(0.8)^3 xx sqrt(2 xx 10 xx 5)` .....(∵ h = 5 m given)
= - (0.8)3 × 10 = - 5.12 m/s
c) Impulse given by the ball during third bounce, is,
J = Δp = mv3 - mv2
= m × (- e3u - e2u)
= - m × e2u × (e + 1)
= - 100 × 10-3 × (0.8)2 × 10 × (0.8 + 1)
= - 1.152 Ns
d) Average force exerted in 250 ms,
F = `"J"/"t" = (- 1.152)/(250 xx 10^-3)`
`= (- 0.1152)/25 xx 10^3`
= – antilog{log (0.1152) – log (25)} × 103
= – antilog{`bar1` .0615 – 1.3979} × 103
= – antilog{`bar3` .6636} × 103
= - 4.609 × 10-3 × 103
= - 4.609 N
e) Average pressure for area
0.5 cm2 = 0.5 × 10-4 m2
P = `"F"/"A" = (4.608)/(0.5 xx 10^-4)`
= 9.216 × 104 N/m2
APPEARS IN
संबंधित प्रश्न
The rate of change of total momentum of a many-particle system is proportional to the ______ on the system.
State if the following statement is true or false. Give a reason for your answer.
In an elastic collision of two bodies, the momentum and energy of each body is conserved.
State if the following statement is true or false. Give a reason for your answer.
Total energy of a system is always conserved, no matter what internal and external forces on the body are present.
Answer carefully, with reason:
Is the total linear momentum conserved during the short time of an elastic collision of two balls?
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following figure is a possible result after collision?

The bob A of a pendulum released from 30° to the vertical hits another bob B of the same mass at rest on a table, as shown in the figure. How high does the bob A rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.

Which of the following potential energy curves in Fig. cannot possibly describe the elastic collision of two billiard balls? Here r is distance between centres of the balls.

Consider the decay of a free neutron at rest : n → p + e–
Show that the two-body decay of this type must necessarily give an electron of fixed energy and, therefore, cannot account for the observed continuous energy distribution in the β-decay of a neutron or a nucleus

Answer the following question.
Obtain its value for an elastic collision and a perfectly inelastic collision.
Solve the following problem.
A spring ball of mass 0.5 kg is dropped from some height. On falling freely for 10 s, it explodes into two fragments of mass ratio 1:2. The lighter fragment continues to travel downwards with a speed of 60 m/s. Calculate the kinetic energy supplied during the explosion.
Define the following:
Coefficient of restitution
Arrive at an expression for elastic collision in one dimension and discuss various cases.
A ball is thrown vertically down from height of 80 m from the ground with an initial velocity 'v'. The ball hits the ground, loses `1/6`th of its total mechanical energy, and rebounds back to the same height. If the acceleration due to gravity is 10 ms-2, the value of 'v' is
A ball moving with velocity 5 m/s collides head on with another stationary ball of double mass. If the coefficient of restitution is 0.8, then their velocities (in m/s) after collision will be ____________.
A block of mass 'm' moving on a frictionless surface at speed 'v' collides elastically with a block of same mass, initially at rest. Now the first block moves at an angle 'θ' with its initial direction and has speed 'v1'. The speed of the second block after collision is ______.
A mass M moving with velocity 'v' along x-axis collides and sticks to another mass 2M which is moving along Y-axis with velocity 3v. After collision, the velocity of the combination is ______.
A wooden block of mass 'M' moves with velocity 'v ' and collides with another block of mass '4M' which is at rest. After collision, the block of mass 'M' comes to rest. The coefficient of restitution will be ______.
A block of mass 'm' moving along a straight line with constant velocity `3vec"v"` collides with another block of same mass at rest. They stick together and move with common velocity. The common velocity is ______.
Two bodies of masses 3 kg and 2 kg collide bead-on. Their relative velocities before and after collision are 20 m/s and 5 m/s respectively. The loss of kinetic energy of the system is ______.
A body of mas 'm' moving with speed 3 m/s collides with a body of mass '2m' at rest. The coalesced mass will start to move with a speed of ______.
A bullet fired from gun with a velocity 30 m/s at an angle of 60° with horizontal direction. At the highest point of its path, the bullet explodes into two parts with masses in the ratio 1:3. The lighter mass comes to rest immediately. Then the speed of the heavier mass is
A ball of mass m, moving with a speed 2v0, collides inelastically (e > 0) with an identical ball at rest. Show that for head-on collision, both the balls move forward.
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
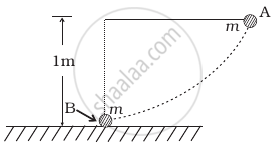
If the length of the pendulum is 1 m, calculate
- the height to which bob A will rise after collision.
- the speed with which bob B starts moving. Neglect the size of the bobs and assume the collision to be elastic.
Two pendulums with identical bobs and lengths are suspended from a common support such that in rest position the two bobs are in contact (Figure). One of the bobs is released after being displaced by 10° so that it collides elastically head-on with the other bob.

- Describe the motion of two bobs.
- Draw a graph showing variation in energy of either pendulum with time, for 0 ≤ t ≤ 2T, where T is the period of each pendulum.
A rod of mass M and length L is lying on a horizontal frictionless surface. A particle of mass 'm' travelling along the surface hits at one end of the rod with velocity 'u' in a direction perpendicular to the rod. The collision is completely elastic. After collision, particle comes to rest. The ratio of masses `(m/M)` is `1/x`. The value of 'x' will be ______.
A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and required 1 s to cover. How long the drunkard takes to fall in a pit 13 m away from the start?
An insect moves with a constant velocity v from one corner of a room to other corner which is opposite of the first corner along the largest diagonal of room. If the insect can not fly and dimensions of room is a × a × a, then the minimum time in which the insect can move is `"a"/"v"`. times the square root of a number n, then n is equal to ______.
The dimension of mutual inductance is ______.
