Advertisements
Advertisements
प्रश्न
Answer the following question.
Obtain its value for an elastic collision and a perfectly inelastic collision.
उत्तर
- Consider a head-on collision of two bodies of masses m1 and m2 with respective initial velocities u1 and u2. As the collision is head-on, the colliding masses are along the same line before and after the collision. The relative velocity of approach is given as,
ua = u2 - u1
Let v1 and v2 be their respective velocities after the collision. The relative velocity of recede (or separation) is then vs = v2 – v1
∴ e = `- "v"_"s"/"u"_"a" = - ("v"_2 - "v"_1)/("u"_2 - "u"_1) = ("v"_1 - "v"_2)/("u"_2 - "u"_1)` .....(1) - For a head-on elastic collision, According to the principle of conservation of linear momentum,
Total initial momentum = Total final momentum
∴ m1u1 + m2u2 = m1v1 + m2v2 ...(2)
∴ m1(u1 - v1) = m2(v2 - u2) ......(3)
As the collision is elastic, the total kinetic energy of the system is also conserved.
∴ `1/2 "m"_1"u"_1^2 + 1/2"m"_2"u"_2^2 = 1/2 "m"_1"v"_1^2 + 1/2 "m"_2"v"_2^2` .....(4)
∴ `"m"_1("u"_1^2 - "v"_1^2) = "m"_2("v"_2^2 - "u"_2^2)`
∴ m1(u1 + v1)(u1 - v1) = m2(v2 + u2)(v2 - u2) .....(5)
Dividing equation (5) by equation (3), we get
u1 + v1 = u2 + v2
∴ u2 - u1 = v1 - v2 .....(6)
Substituting this in equation (1),
e = `("v"_1 - "v"_2)/("u"_2 - "u"_1)` = 1 - For a perfectly inelastic collision, the colliding bodies move jointly after the collision, i.e.,
v1 = v2
∴ v1 - v2 = 0
Substituting this in equation (1),
e = 0
APPEARS IN
संबंधित प्रश्न
State if the following statement is true or false. Give a reason for your answer.
In an elastic collision of two bodies, the momentum and energy of each body is conserved.
State if the following statement is true or false. Give a reason for your answer.
Total energy of a system is always conserved, no matter what internal and external forces on the body are present.
Answer carefully, with reason:
In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?
Answer carefully, with reason:
In an inelastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e., when they are in contact)?
Answer carefully, with reason:
If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic? (Note, we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy.)
Which of the following potential energy curves in Fig. cannot possibly describe the elastic collision of two billiard balls? Here r is distance between centres of the balls.

Consider the decay of a free neutron at rest : n → p + e–
Show that the two-body decay of this type must necessarily give an electron of fixed energy and, therefore, cannot account for the observed continuous energy distribution in the β-decay of a neutron or a nucleus

Solve the following problem.
A ball of mass 100 g dropped on the ground from 5 m bounces repeatedly. During every bounce, 64% of the potential energy is converted into kinetic energy. Calculate the following:
- Coefficient of restitution.
- The speed with which the ball comes up from the ground after the third bounce.
- The impulse was given by the ball to the ground during this bounce.
- Average force exerted by the ground if this impact lasts for 250 ms.
- The average pressure exerted by the ball on the ground during this impact if the contact area of the ball is 0.5 cm2.
Explain the characteristics of elastic and inelastic collision.
Define the following:
Coefficient of restitution
A ball moving with velocity 5 m/s collides head on with another stationary ball of double mass. If the coefficient of restitution is 0.8, then their velocities (in m/s) after collision will be ____________.
A bomb of mass 9 kg explodes into two pieces of mass 3 kg and 6 kg. The velocity of mass 3 kg is 16 m/s, The kinetic energy of mass 6 kg is ____________.
In inelastic collision, ____________.
A wooden block of mass 'M' moves with velocity 'v ' and collides with another block of mass '4M' which is at rest. After collision, the block of mass 'M' comes to rest. The coefficient of restitution will be ______.
A block of mass 'm' moving along a straight line with constant velocity `3vec"v"` collides with another block of same mass at rest. They stick together and move with common velocity. The common velocity is ______.
A body of mas 'm' moving with speed 3 m/s collides with a body of mass '2m' at rest. The coalesced mass will start to move with a speed of ______.
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V as shown in figure.
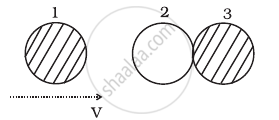
If the collision is elastic, which of the following (Figure) is a possible result after collision?
A cricket ball of mass 150 g moving with a speed of 126 km/h hits at the middle of the bat, held firmly at its position by the batsman. The ball moves straight back to the bowler after hitting the bat. Assuming that collision between ball and bat is completely elastic and the two remain in contact for 0.001s, the force that the batsman had to apply to hold the bat firmly at its place would be ______.
A ball of mass m, moving with a speed 2v0, collides inelastically (e > 0) with an identical ball at rest. Show that for a general collision, the angle between the two velocities of scattered balls is less than 90°.
Consider a one-dimensional motion of a particle with total energy E. There are four regions A, B, C and D in which the relation between potential energy V, kinetic energy (K) and total energy E is as given below:
Region A : V > E
Region B : V < E
Region C : K > E
Region D : V > K
State with reason in each case whether a particle can be found in the given region or not.
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
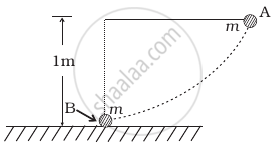
If the length of the pendulum is 1 m, calculate
- the height to which bob A will rise after collision.
- the speed with which bob B starts moving. Neglect the size of the bobs and assume the collision to be elastic.
A rod of mass M and length L is lying on a horizontal frictionless surface. A particle of mass 'm' travelling along the surface hits at one end of the rod with velocity 'u' in a direction perpendicular to the rod. The collision is completely elastic. After collision, particle comes to rest. The ratio of masses `(m/M)` is `1/x`. The value of 'x' will be ______.
A ball is thrown upwards from the foot of a tower. The ball crosses the top of tower twice after an interval of 4 seconds and the ball reaches ground after 8 seconds, then the height of tower is ______ m. (g = 10 m/s2)
A sphere of mass 'm' moving with velocity 'v' collides head-on another sphere of same mass which is at rest. The ratio of final velocity of second sphere to the initial velocity of the first sphere is ______. ( e is coefficient of restitution and collision is inelastic)
