Advertisements
Advertisements
Question
Solve the following problem.
A ball of mass 100 g dropped on the ground from 5 m bounces repeatedly. During every bounce, 64% of the potential energy is converted into kinetic energy. Calculate the following:
- Coefficient of restitution.
- The speed with which the ball comes up from the ground after the third bounce.
- The impulse was given by the ball to the ground during this bounce.
- Average force exerted by the ground if this impact lasts for 250 ms.
- The average pressure exerted by the ball on the ground during this impact if the contact area of the ball is 0.5 cm2.
Solution
Given that, for every bounce, 64% of the initial energy is converted to final energy.
a) Coefficient of restitution in case of inelastic collision is given by,
e = `- "v"_"s"/"u"_"a" = - "v"/"u"` ....(1)
∴ `"e"^2 = "v"^2/"u"^2`
∴ v2 = e2 × u2
∴ `1/2 "mv"^2 = "e"^2 xx 1/2 "mu"^2`
∴ (K.E.)f = e2 × `1/2` mu2
∴ `("K.E.")_"f"/("K.E.")_"i" = "e"^2`
∴ `64/100 = "e"^2`
∴ e = 0.8
b) From equation (1),
v = – eu
∴ After first bounce,
v1 = - eu
after second bounce,
v2 = - ev1 = - e(- eu) = e2u
and after third bounce,
v3 = - ev2 = - e(- e2u) = - e3u
But u = `sqrt(2"gh")`
∴ `"v"_3 = - "e"^3 xx sqrt(2"gh") = -(0.8)^3 xx sqrt(2 xx 10 xx 5)` .....(∵ h = 5 m given)
= - (0.8)3 × 10 = - 5.12 m/s
c) Impulse given by the ball during third bounce, is,
J = Δp = mv3 - mv2
= m × (- e3u - e2u)
= - m × e2u × (e + 1)
= - 100 × 10-3 × (0.8)2 × 10 × (0.8 + 1)
= - 1.152 Ns
d) Average force exerted in 250 ms,
F = `"J"/"t" = (- 1.152)/(250 xx 10^-3)`
`= (- 0.1152)/25 xx 10^3`
= – antilog{log (0.1152) – log (25)} × 103
= – antilog{`bar1` .0615 – 1.3979} × 103
= – antilog{`bar3` .6636} × 103
= - 4.609 × 10-3 × 103
= - 4.609 N
e) Average pressure for area
0.5 cm2 = 0.5 × 10-4 m2
P = `"F"/"A" = (4.608)/(0.5 xx 10^-4)`
= 9.216 × 104 N/m2
APPEARS IN
RELATED QUESTIONS
State if the following statement is true or false. Give a reason for your answer.
Total energy of a system is always conserved, no matter what internal and external forces on the body are present.
Answer carefully, with reason:
In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?
Answer carefully, with reason:
In an inelastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e., when they are in contact)?
Answer carefully, with reason:
If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic? (Note, we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy.)
A bullet of mass 0.012 kg and horizontal speed 70 m s–1 strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
Consider the decay of a free neutron at rest : n → p + e–
Show that the two-body decay of this type must necessarily give an electron of fixed energy and, therefore, cannot account for the observed continuous energy distribution in the β-decay of a neutron or a nucleus

Define coefficient of restitution.
Answer the following question.
Discuss the following as special cases of elastic collisions and obtain their exact or approximate final velocities in terms of their initial velocities.
- Colliding bodies are identical.
- A very heavy object collides on a lighter object, initially at rest.
- A very light object collides on a comparatively much massive object, initially at rest.
Answer the following question.
A bullet of mass m1 travelling with a velocity u strikes a stationary wooden block of mass m2 and gets embedded into it. Determine the expression for loss in the kinetic energy of the system. Is this violating the principle of conservation of energy? If not, how can you account for this loss?
Solve the following problem.
A spring ball of mass 0.5 kg is dropped from some height. On falling freely for 10 s, it explodes into two fragments of mass ratio 1:2. The lighter fragment continues to travel downwards with a speed of 60 m/s. Calculate the kinetic energy supplied during the explosion.
Solve the following problem.
A marble of mass 2m travelling at 6 cm/s is directly followed by another marble of mass m with double speed. After a collision, the heavier one travels with the average initial speed of the two. Calculate the coefficient of restitution.
A block of mass 'm' moving on a frictionless surface at speed 'v' collides elastically with a block of same mass, initially at rest. Now the first block moves at an angle 'θ' with its initial direction and has speed 'v1'. The speed of the second block after collision is ______.
A bomb of mass 9 kg explodes into two pieces of mass 3 kg and 6 kg. The velocity of mass 3 kg is 16 m/s, The kinetic energy of mass 6 kg is ____________.
In inelastic collision, ____________.
A particle of mass 'm' collides with another stationary particle of mass 'M'. A particle of mass 'm' stops just after collision. The coefficient of restitution is ______.
A smooth sphere of mass 'M' moving with velocity 'u' directly collides elastically with another sphere of mass 'm' at rest. After collision, their final velocities are V' and V respectively. The value of V is given by ______.
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V as shown in figure.
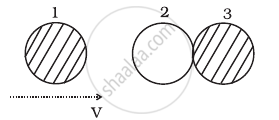
If the collision is elastic, which of the following (Figure) is a possible result after collision?
A cricket ball of mass 150 g moving with a speed of 126 km/h hits at the middle of the bat, held firmly at its position by the batsman. The ball moves straight back to the bowler after hitting the bat. Assuming that collision between ball and bat is completely elastic and the two remain in contact for 0.001s, the force that the batsman had to apply to hold the bat firmly at its place would be ______.
A ball of mass m, moving with a speed 2v0, collides inelastically (e > 0) with an identical ball at rest. Show that for head-on collision, both the balls move forward.
A ball of mass m, moving with a speed 2v0, collides inelastically (e > 0) with an identical ball at rest. Show that for a general collision, the angle between the two velocities of scattered balls is less than 90°.
Two pendulums with identical bobs and lengths are suspended from a common support such that in rest position the two bobs are in contact (Figure). One of the bobs is released after being displaced by 10° so that it collides elastically head-on with the other bob.

- Describe the motion of two bobs.
- Draw a graph showing variation in energy of either pendulum with time, for 0 ≤ t ≤ 2T, where T is the period of each pendulum.
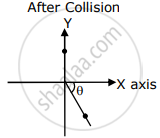
A ball of mass 10 kg moving with a velocity of 10`sqrt3` ms–1 along the X-axis, hits another ball of mass 20 kg which is at rest. After collision, the first ball comes to rest and the second one disintegrates into two equal pieces. One of the pieces starts moving along Y-axis at a speed of 10 m/s. The second piece starts moving at a speed of 20 m/s at an angle θ (degree) with respect to the X-axis.
The configuration of pieces after the collision is shown in the figure.
The value of θ to the nearest integer is ______.
A particle of mass m with an initial velocity u`hat"i"` collides perfectly elastically with a mass 3m at rest. It moves with a velocity v`hat"j"` after collision, then, v is given by :
A ball is thrown upwards from the foot of a tower. The ball crosses the top of tower twice after an interval of 4 seconds and the ball reaches ground after 8 seconds, then the height of tower is ______ m. (g = 10 m/s2)
An alpha-particle of mass m suffers 1-dimensional elastic collision with a nucleus at rest of unknown mass. It is scattered directly backwards losing, 64% of its initial kinetic energy. The mass of the nucleus is ______.
The dimension of mutual inductance is ______.
A sphere of mass 'm' moving with velocity 'v' collides head-on another sphere of same mass which is at rest. The ratio of final velocity of second sphere to the initial velocity of the first sphere is ______. ( e is coefficient of restitution and collision is inelastic)
Three identical blocks A, B and C are placed on horizontal frictionless surface. The blocks A and C are at rest. But A is approaching towards B with a speed 10 m/s. The coefficient of restitution for all collision is 0.5. The speed of the block C just after the collision is ______.

