Advertisements
Advertisements
Question
Define coefficient of restitution.
Solution
For two colliding bodies, the negative of the ratio of the relative velocity of separation to the relative velocity of approach is called the coefficient of restitution.
APPEARS IN
RELATED QUESTIONS
In an inelastic collision of two bodies, the quantities which do not change after the collision are the ______ of the system of two bodies.
State if the following statement is true or false. Give a reason for your answer.
Total energy of a system is always conserved, no matter what internal and external forces on the body are present.
State if the following statement is true or false. Give a reason for your answer.
In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system.
Answer carefully, with reason:
Is the total linear momentum conserved during the short time of an elastic collision of two balls?
Answer carefully, with reason:
In an inelastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e., when they are in contact)?
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following figure is a possible result after collision?

The bob A of a pendulum released from 30° to the vertical hits another bob B of the same mass at rest on a table, as shown in the figure. How high does the bob A rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.

Which of the following potential energy curves in Fig. cannot possibly describe the elastic collision of two billiard balls? Here r is distance between centres of the balls.

Solve the following problem.
A spring ball of mass 0.5 kg is dropped from some height. On falling freely for 10 s, it explodes into two fragments of mass ratio 1:2. The lighter fragment continues to travel downwards with a speed of 60 m/s. Calculate the kinetic energy supplied during the explosion.
Explain the characteristics of elastic and inelastic collision.
What is inelastic collision? In which way it is different from an elastic collision. Mention a few examples in day-to-day life for inelastic collision.
A ball moving with velocity 5 m/s collides head on with another stationary ball of double mass. If the coefficient of restitution is 0.8, then their velocities (in m/s) after collision will be ____________.
A block of mass 'm' moving on a frictionless surface at speed 'v' collides elastically with a block of same mass, initially at rest. Now the first block moves at an angle 'θ' with its initial direction and has speed 'v1'. The speed of the second block after collision is ______.
A particle of mass 'm' collides with another stationary particle of mass 'M'. A particle of mass 'm' stops just after collision. The coefficient of restitution is ______.
A wooden block of mass 'M' moves with velocity 'v ' and collides with another block of mass '4M' which is at rest. After collision, the block of mass 'M' comes to rest. The coefficient of restitution will be ______.
Two bodies of masses 3 kg and 2 kg collide bead-on. Their relative velocities before and after collision are 20 m/s and 5 m/s respectively. The loss of kinetic energy of the system is ______.
A bullet fired from gun with a velocity 30 m/s at an angle of 60° with horizontal direction. At the highest point of its path, the bullet explodes into two parts with masses in the ratio 1:3. The lighter mass comes to rest immediately. Then the speed of the heavier mass is
During inelastic collision between two bodies, which of the following quantities always remain conserved?
Two pendulums with identical bobs and lengths are suspended from a common support such that in rest position the two bobs are in contact (Figure). One of the bobs is released after being displaced by 10° so that it collides elastically head-on with the other bob.

- Describe the motion of two bobs.
- Draw a graph showing variation in energy of either pendulum with time, for 0 ≤ t ≤ 2T, where T is the period of each pendulum.
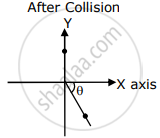
A ball of mass 10 kg moving with a velocity of 10`sqrt3` ms–1 along the X-axis, hits another ball of mass 20 kg which is at rest. After collision, the first ball comes to rest and the second one disintegrates into two equal pieces. One of the pieces starts moving along Y-axis at a speed of 10 m/s. The second piece starts moving at a speed of 20 m/s at an angle θ (degree) with respect to the X-axis.
The configuration of pieces after the collision is shown in the figure.
The value of θ to the nearest integer is ______.
A particle of mass m with an initial velocity u`hat"i"` collides perfectly elastically with a mass 3m at rest. It moves with a velocity v`hat"j"` after collision, then, v is given by :
A ball is thrown upwards from the foot of a tower. The ball crosses the top of tower twice after an interval of 4 seconds and the ball reaches ground after 8 seconds, then the height of tower is ______ m. (g = 10 m/s2)
The dimension of mutual inductance is ______.
A sphere of mass 'm' moving with velocity 'v' collides head-on another sphere of same mass which is at rest. The ratio of final velocity of second sphere to the initial velocity of the first sphere is ______. ( e is coefficient of restitution and collision is inelastic)
