Advertisements
Advertisements
प्रश्न
The activation energy for the reaction \[\ce{2 HI_{(g)} -> H2_{(g)} + I2_{(g)}}\] is 209.5 kJ mol−1 at 581K. Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy?
उत्तर
In the given case:
Ea = 209.5 kJ mol−1
T = 581 K
R = 8.314 JK−1 mol−1
Now, the fraction of molecules of reactants having energy equal to or greater than activation energy is given as:
x = `"n"/"N"`
x = `e^((-E_a)/"RT")`
In x = `- (E_a)/"RT"`
or, log x = `-E_a/(2.303 "RT")`
or, log x = `-(209.5 xx 10^3 "J mol"^-1)/(2.303 xx 8.314 "JK"^-1 "mol"^-1 xx 581 "K")`
= −18.8323
x = antilog (−18.8323)
= antilog 19.1677
= 1.471 × 10−19
APPEARS IN
संबंधित प्रश्न
(b) Rate constant ‘k’ of a reaction varies with temperature ‘T’ according to the equation:
`logk=logA-E_a/2.303R(1/T)`
Where Ea is the activation energy. When a graph is plotted for `logk Vs. 1/T` a straight line with a slope of −4250 K is obtained. Calculate ‘Ea’ for the reaction.(R = 8.314 JK−1 mol−1)
The rate constant of a first order reaction increases from 4 × 10−2 to 8 × 10−2 when the temperature changes from 27°C to 37°C. Calculate the energy of activation (Ea). (log 2 = 0.301, log 3 = 0.4771, log 4 = 0.6021)
The rate constant for the first-order decomposition of H2O2 is given by the following equation:
`logk=14.2-(1.0xx10^4)/TK`
Calculate Ea for this reaction and rate constant k if its half-life period be 200 minutes.
(Given: R = 8.314 JK–1 mol–1)
What will be the effect of temperature on rate constant?
The rate of the chemical reaction doubles for an increase of 10 K in absolute temperature from 298 K. Calculate Ea.
The rate constant for the decomposition of N2O5 at various temperatures is given below:
| T/°C | 0 | 20 | 40 | 60 | 80 |
| 105 × k/s−1 | 0.0787 | 1.70 | 25.7 | 178 | 2140 |
Draw a graph between ln k and `1/"T"` and calculate the values of A and Ea. Predict the rate constant at 30º and 50ºC.
Consider a certain reaction \[\ce{A -> Products}\] with k = 2.0 × 10−2 s−1. Calculate the concentration of A remaining after 100 s if the initial concentration of A is 1.0 mol L−1.
The decomposition of A into product has value of k as 4.5 × 103 s−1 at 10°C and energy of activation 60 kJ mol−1. At what temperature would k be 1.5 × 104 s−1?
The rate of a reaction quadruples when the temperature changes from 293 K to 313 K. Calculate the energy of activation of the reaction assuming that it does not change with temperature.
The chemical reaction in which reactants require high amount of activation energy are generally ____________.
Which of the following graphs represents exothermic reaction?
(a)
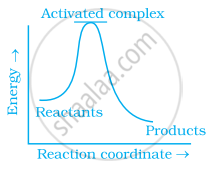
(b)
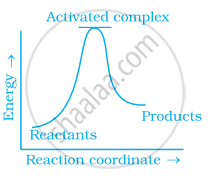
(c)
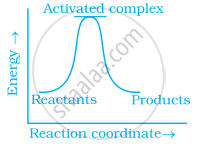
During decomposition of an activated complex:
(i) energy is always released
(ii) energy is always absorbed
(iii) energy does not change
(iv) reactants may be formed
The activation energy in a chemical reaction is defined as ______.
The equation k = `(6.5 xx 10^12 "s"^(-1))"e"^(- 26000 " K"//"T")` is followed for the decomposition of compound A. The activation energy for the reaction is ______ kJ mol-1. (Nearest integer) (Given: R = 8.314 JK-1 mol-1)
The decomposition of N2O into N2 and O2 in the presence of gaseous argon follows second-order kinetics, with k = (5.0 × 1011 L mol−1 s−1) `"e"^(-(29000 "K")/"T")`. Arrhenius parameters are ______ kJ mol−1.
An exothermic reaction X → Y has an activation energy 30 kJ mol-1. If energy change ΔE during the reaction is - 20 kJ, then the activation energy for the reverse reaction in kJ is ______.
A schematic plot of ln Keq versus inverse of temperature for a reaction is shown below
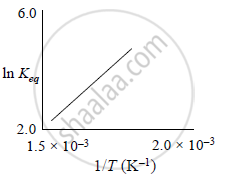
The reaction must be:
What happens to the rate constant k and activation energy Ea as the temperature of a chemical reaction is increased? Justify.
