Question

The annual rainfall record of a city for 66 days is given in the following table :

Rainfall (in cm ):	0-10	10-20	20-30	30-40	40-50	50-60
Number of days :	22	10	8	15	5	6

Calculate the median rainfall using ogives of more than type and less than type.

Answer 1

Prepare a table for less than type.

Rainfall (in cm)	Number of Days	Rainfall (Less Than)	Cumulative Frequency	Suitable Points
0−10	22	10	22	(10, 22)
10−20	10	20	32	(20, 32)
20−30	8	30	40	(30, 40)
30−40	15	40	55	(40, 55)
40−50	5	50	60	(50, 60)
50−60	6	60	66	(60, 66)

Now, plot the less than ogive using suitable points.

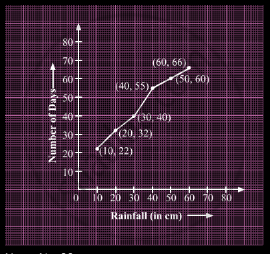
Here, N = 66.

\[\therefore \frac{N}{2} = 33\]

In order to find the median rainfall, we first locate the point corresponding to 33rd day on the y-axis. Let the point be P. From this point draw a line parallel to the x-axis cutting the curve at Q. From this point Q, draw a line parallel to the y-axis and meeting the x-axis at the point R. The x-coordinate of R is 21.25.

Thus, the median rainfall is 21.25 cm.

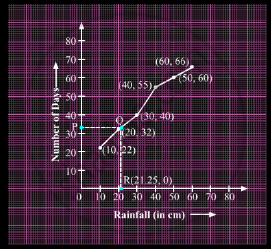
Let us now prepare a table for more than type.

Rainfall (in cm)	Number of Days	Rainfall (More Than)	Cumulative Frequency	Suitable Points
0−10	22	0	66(0, 66)	(0, 66)
10−20	10	10	44	(10, 44)
20−30	8	20	34	(20, 34)
30−40	15	30	26	(30, 26)
40−50	5	40	11	(40, 11)
50−60	6	50	6	(50, 6)

Now, plot the more than ogive with suitable points.

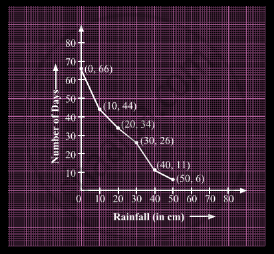
Here, N = 66.

\[\therefore \frac{N}{2} = 33\]

In order to find the median rainfall, we first locate the point corresponding to 33rd day on the y-axis. Let the point be P. From this point draw a line parallel to the x-axis cutting the curve at Q. From this point Q, draw a line parallel to the y-axis and meeting the x-axis at the point R. The x-coordinate of R is 21.25.

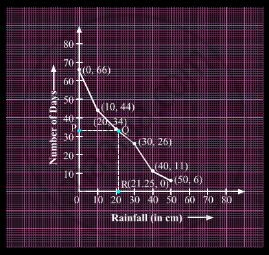
Thus, the median rainfall is 21.25 cm.