Advertisements
Advertisements
Question
The annual rainfall record of a city for 66 days is given in the following table :
| Rainfall (in cm ): | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| Number of days : | 22 | 10 | 8 | 15 | 5 | 6 |
Calculate the median rainfall using ogives of more than type and less than type.
Solution
Prepare a table for less than type.
| Rainfall (in cm) |
Number of Days |
Rainfall (Less Than) |
Cumulative Frequency |
Suitable Points |
| 0−10 | 22 | 10 | 22 | (10, 22) |
| 10−20 | 10 | 20 | 32 | (20, 32) |
| 20−30 | 8 | 30 | 40 | (30, 40) |
| 30−40 | 15 | 40 | 55 | (40, 55) |
| 40−50 | 5 | 50 | 60 | (50, 60) |
| 50−60 | 6 | 60 | 66 | (60, 66) |
Now, plot the less than ogive using suitable points.
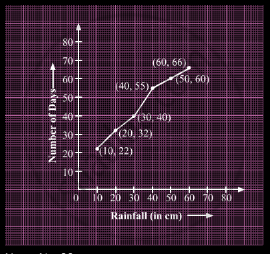
Here, N = 66.
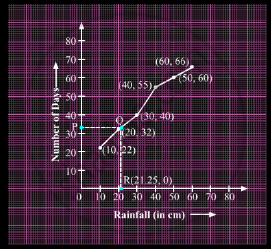
Let us now prepare a table for more than type.
| Rainfall (in cm) |
Number of Days |
Rainfall (More Than) |
Cumulative Frequency |
Suitable Points |
| 0−10 | 22 | 0 | 66(0, 66) | (0, 66) |
| 10−20 | 10 | 10 | 44 | (10, 44) |
| 20−30 | 8 | 20 | 34 | (20, 34) |
| 30−40 | 15 | 30 | 26 | (30, 26) |
| 40−50 | 5 | 40 | 11 | (40, 11) |
| 50−60 | 6 | 50 | 6 | (50, 6) |
Now, plot the more than ogive with suitable points.
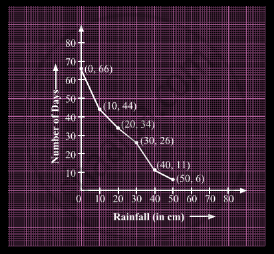
Here, N = 66.
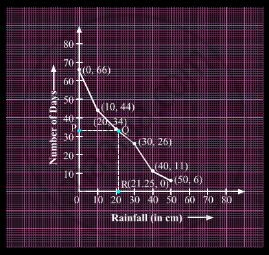
Thus, the median rainfall is 21.25 cm.
APPEARS IN
RELATED QUESTIONS
Calculate the median from the following data:
| Marks below: | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| No. of students: | 15 | 35 | 60 | 84 | 96 | 127 | 198 | 250 |
Find the missing frequencies and the median for the following distribution if the mean is 1.46.
| No. of accidents: | 0 | 1 | 2 | 3 | 4 | 5 | Total |
| Frequency (No. of days): | 46 | ? | ? | 25 | 10 | 5 | 200 |
A student got the following marks in 9 questions of a question paper.
3, 5, 7, 3, 8, 0, 1, 4 and 6.
Find the median of these marks.
The ages of 37 students in a class are given in the following table:
| Age (in years) | 11 | 12 | 13 | 14 | 15 | 16 |
| Frequency | 2 | 4 | 6 | 10 | 8 | 7 |
A data has 25 observations arranged in a descending order. Which observation represents the median?
In the following table, Σf = 200 and mean = 73. Find the missing frequencies f1, and f2.
| x | 0 | 50 | 100 | 150 | 200 | 250 |
| f | 46 | f1 | f2 | 25 | 10 | 5 |
The Median when it is given that mode and mean are 8 and 9 respectively, is ______.
Find the median of the following frequency distribution:
| Class: | 0 – 20 | 20 – 40 | 40 – 60 | 60 – 80 | 80 – 100 |
| Frequency: | 6 | 8 | 5 | 9 | 7 |
If in a frequency distribution, the mean and median are 21 and 22 respectively, then its mode is approximately ______.
Consider the following frequency distribution:
| Class | 0 – 6 | 6 – 12 | 12 – 18 | 18 – 24 | 24 – 30 |
| Frequency | 12 | 10 | 15 | 8 | 11 |
The median class is:
