Advertisements
Advertisements
प्रश्न
The mean of five numbers is 27. If one number is excluded, the mean of the remaining numbers is 25. Find the excluded number.
उत्तर
The mean of 5 observations = 27
Total sum of 5 observations = 27 × 5 = 135
On excluding an observation, the mean of the remaining 4 observations = 25
⇒ Total of remaining 4 observations = 25 × 4 = 100
⇒ Included observation = Total mean of 5 observations – Total mean of 4 observations
= 135 − 100 = 35
APPEARS IN
संबंधित प्रश्न
Using the information given in the adjoining histogram, calculate the mean.
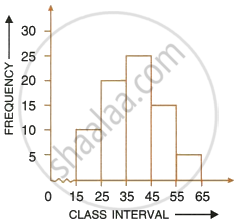
Draw a histogram and hence estimate the mode for the following frequency distribution:
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| Freq | 2 | 8 | 10 | 5 | 4 | 3 |
Find the mode and the median of the following frequency distributions.
| x | 10 | 11 | 12 | 13 | 14 | 15 |
| f | 1 | 4 | 7 | 5 | 9 | 3 |
Find the mode of the following:
15, 17, 16, 17, 10, 12, 14, 16, 19, 12, 16, 15, 16
Find the mode of the following frequency distribution:
| Pocket money per week in Rs | 25 | 50 | 75 | 100 | 125 | 150 |
| No. of students | 4 | 7 | 13 | 18 | 6 | 2 |
Draw a histogram for the following distribution and estimate the mode:
| I.Q. Score | 80-100 | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 |
| No. of Students | 6 | 9 | 16 | 13 | 4 | 2 |
Find the median of 17, 23, 36, 12, 18, 23, 40 and 20
Calculate the median of the following sets of number:
1, 9, 10, 8, 2, 4, 4, 3, 9, 1, 5, 6, 2 and 4.
The median first 6 odd natural numbers is ____________
Find the median of first nine even natural numbers.
