Advertisements
Advertisements
प्रश्न
Two masses 8 kg and 12 kg are connected at the two ends of a light, inextensible string that goes over a frictionless pulley. Find the acceleration of the masses, and the tension in the string when the masses are released.
उत्तर
The given system of two masses and a pulley can be represented as shown in the following figure:
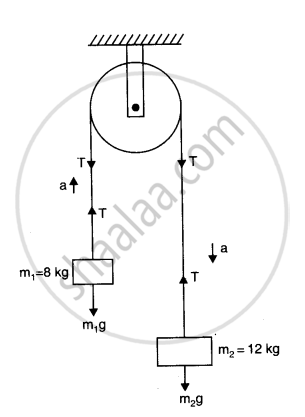
Smaller mass, m1 = 8 kg
Larger mass, m2 = 12 kg
Tension in the string = T
Mass m2, owing to its weight, moves downward with acceleration a,and mass m1moves upward.
Applying Newton’s second law of motion to the system of each mass:
For mass m1:
The equation of motion can be written as:
T – m1g = ma … (i)
For mass m2:
The equation of motion can be written as:
m2g – T = m2a … (ii)
Adding equations (i) and (ii), we get:
(m_2-m_1)g = (m_1+ m_2)a
`:.a = ((m_2-m_1)/(m_1+m_2))g ...(iii)`
`=((12-8)/(12+8)) xx 10= 4/20 xx 10 = 2 "m/s"^2`
Therefore, the acceleration of the masses is 2 m/s2.
Substituting the value of a in equation (ii), we get:
`m_2g - T = m_2 ( (m_2-m_1)/(m_1+m_2))g`
`=((2m_1m_2)/(m_1+m_2))g`
`=(2xx12xx8)/(12+8)xx10`
`=(2xx12xx8)/20 xx 10 = 96 N`
Therefore, the tension in the string is 96 N.
APPEARS IN
संबंधित प्रश्न
A smooth wedge A is fitted in a chamber hanging from a fixed ceiling near the earth's surface. A block B placed at the top of the wedge takes time T to slide down the length of the wedge. If the block is placed at the top of the wedge and the cable supporting the chamber is broken at the same instant, the block will.
A person is standing on a weighing machine placed on the floor of an elevator. The elevator starts going up with some acceleration, moves with uniform velocity for a while and finally decelerates to stop. The maximum and the minimum weights recorded are 72 kg and 60 kg, respectively. Assuming that the magnitudes of acceleration and deceleration are the same, find (a) the true weight of the person and (b) the magnitude of the acceleration. Take g = 9.9 m/s2.
Suppose the ceiling in the previous problem is that of an elevator which is going up with an acceleration of 2.0 m/s2. Find the elongation.
An empty plastic box of mass m is found to accelerate up at the rate of g/6 when placed deep inside water. How much sand should be put inside the box so that it may accelerate down at the rate of g/6?
Consider the Atwood machine of the previous problem. The larger mass is stopped for a moment, 2.0 s after the system is set into motion. Find the time that elapses before the string is tight again.
In the following figure shows a uniform rod of length 30 cm and mass 3.0 kg. The strings shown in the figure are pulled by constant forces of 20 N and 32 N. Find the force exerted by the 20 cm part of the rod on the 10 cm part. All the surfaces are smooth and the strings and the pulleys are light.

Show that the rate of change of momentum = mass × acceleration. Under what condition does this relation hold?
A pebble is thrown vertically upwards with a speed of 20 m s-1. How high will it be after 2 s? (Take g = 10 m s-2)
A stone is dropped from a cliff 98 m high.
How long will it take to fall to the foot of the cliff?
In the previous problem (5.3), the magnitude of the momentum transferred during the hit is ______.
