Advertisements
Advertisements
प्रश्न
Water flows at the rate of 10 meters per minute through a cylindrical pipe having its diameter 20 mm. how much time will it take to fill a conical vessel of diameter 40 cm and depth 24 cm?
उत्तर
For the cylindrical pipe:
diameter = 20 mm
∴ radius = ` "diameter"/2 = 20/2` = 10 mm = 1cm
Rate of flow of water through the pipe = 10m/minute
= 10 × 100 cm /minute
= 1000 cm/minute
∴ Water flow's through a distance (h) of 1000 cm in a minute
volume of water flowing through the pipe in 1 minute = `pir^2h`
= π × 1× 1× 1000
= 1000π cm3
For the conical vessel:
diameter = 40 cm
∴ radius =`"diameter"/2 = 40/2 = 20` cm
depth (h) = 24cm
Volume of conical vessel = `1/3 pi r^2h`
`= (1/3xx pi xx 20 xx20xx24)` cm3
Time is taken to fill the conical vessel =`" volume of conical vessel"/"volume of water flowing through a pipe in 1 min"`
`= (1/3 xx pi xx 20xx20xx24)/(1000pi)`
`= (pi xx 20xx20xx24)/(3xxpixx1000)`
`= 3200/1000 = `3.2 minutes
∴ Time taken to fill the conical veseel is 3.2 minutes.
APPEARS IN
संबंधित प्रश्न
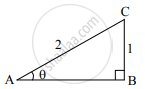
In the following figure, in ΔABC, BC = 1, AC = 2, ∠B = 90°. Find the value of sin θ.
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree. (Use `sqrt(3)` = 1.732)
A ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2 m away from the wall and the ladder is making an angle of 60° with the level of the ground. Determine the height of the wall.
The length of a string between a kite and a point on the ground is 90 meters. If the string makes an angle O with the ground level such that tan O = 15/8, how high is the kite? Assume that there is no slack in the string.
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
An observer 1.5m tall is 30 away from a chimney. The angle of elevation of the top of the chimney from his eye is 60 . Find the height of the chimney.
The angle of elevation of the top of a chimney form the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30° . If the height of the tower is 40 meters. Find the height of the chimney.
From the top of a hill, the angles of depression of two consecutive kilometer stones due east are found to be 45° and 30° respectivly. Find the height of the hill ?
A vessel full of water is in the form of an inverted cone of height 8 cm and the radius of its top, which is open, is 5 cm. 100 spherical lead balls are dropped into the vessel. One-fourth of the water flows out of the vessel. Find the radius of a spherical ball ?
From the top of a tree of height 13 m the angle of elevation and depression of the top and bottom of another tree are 45° and 30° respectively. Find the height of the second tree. `(sqrt(3) = 1.732)`
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the difference between height of the lamp post and the apartment
A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45°. The bird flies away horizontally in such away that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30°. Determine the speed at which the bird flies `(sqrt(3) = 1.732)`
An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37°. After what period of time does the angle of elevation increase to 53°? (tan 53° = 1.3270, tan 37° = 0.7536)
At some time of the day, the length of the shadow of a tower is equal to its height. Then, the sun’s altitude at that time is ______.
In given Fig., the angle of depression from the observing position D and E of the object at A are ____________.
An observer 1.5 m tall is 28.5 m away from a tower. The angle of elevation of the top of the tower from her eyes is 45°. What is the height of the tower?
An electrician has to repair an electric fault on a pole of height 4 m. He needs to reach a point 1.3 m below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
Two towers A and B are standing some distance apart. From the top of tower A, the angle of depression of the foot of tower B is found to be 30°. From the top of tower B, the angle of depression of the foot of tower A is found to be 60°. If the height of tower B is ‘h’ m then the height of tower A in terms of ‘h’ is ____________ m.
From the top of an 8 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Take `sqrt(3)` = 1.732).
The top of a hill when observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. What is the height of the hill?
