Advertisements
Advertisements
प्रश्न
While driving along an unbanked circular road, a two-wheeler rider has to lean with the vertical. Why is it so? With what angle the rider has to lean? Derive the relevant expression. Why such a leaning is not necessary for a four wheeler?
उत्तर
(i) When a bicyclist takes a turn along an unbanked road, the force of friction `vec"f"_"s"` provides the centripetal force; the normal reaction of the road `vec"N"` is vertically up. If the bicyclist does not lean inward, there will be an unbalanced outward torque about the centre of gravity, fs·h, due to the friction force that will topple the bicyclist outward. The bicyclist must lean inward to counteract this torque (and not to generate a centripetal force) such that the opposite inward torque of the couple formed by `vec"N"` and the weight `vec"g"`, mg.a = fs.h1
| (a) | (b) |
 |
 |
A bicyclist taking a turn to his left on a level road
(ii) Since the force of friction provides the centripetal force,
fs = `"mv"^2/"r"`
If the cyclist leans from the vertical by an angle θ, the angle between `vec"N"` and `vec"F"`
tan θ = `"f"_"s"/"N" = ("mv"^2//"r")/"mg" = "v"^2/"gr"`
Hence, the cyclist must lean by an angle
θ = tan-1 `("v"^2/"gr")`
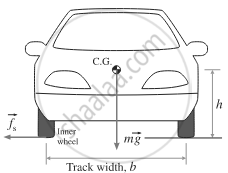
(iii) When a car takes a turn along a level road, apart from the risk of skidding off outward, it also has a tendency to roll outward due to an outward torque about the Centre of gravity due to the friction force. But a car is an extended object with four wheels. So, when the inner wheels just get lifted above the ground, it can be counterbalanced by a restoring torque of the couple formed by the normal reaction (on the outer wheels) and the weight. Consider a car of mass m taking a turn of radius r along a level road. As seen from an inertial frame of reference, the forces acting on the car are:
(1) the lateral limiting force of static friction `vec"f"_"s"` on the wheels – acting along the axis of the wheels and towards the center of the circular path which provides the necessary centripetal force.
(2) the weight `vec"m""g"` acting vertically downwards at the centre of gravity (C.G.)
(3) the normal reaction `vec"N"` of the road on the wheels, upwards effectively at the C.G. Since maximum centripetal force = limiting force of static friction,
`"ma"_"r" = "mv"^2/"r" = "f"_"s"` ...(1)
In a simplified rigid-body vehicle model, we consider only two parameters – the height h of the C.G. above the ground and the average distance b between the left and right wheels called the track width.
| (a) | (b) | (c) |
 |
 |
 |
Rolling tendency of a vehicle negotiating a bend on a level road
The friction force `vec"f"_"s"` on the wheels produces a torque `tau_"t"` that tends to overturn/rollover the car about the outer wheel in the above figure (b). Rotation about the front-to-back axis is called roll.
`tau_"t" = "f"_"s"."h" = ("mv"^2/"r")"h"` ...(2)
When the inner wheel just gets lifted above the ground, the normal reaction `vec"N"` of the road acts on the outer wheels but the weight continues to act at the C.G. Then, the couple formed by the normal reaction and the weight produces a opposite torque `tau_"r"` which tends to restore the car back on all four wheels in the above figure (b).
`tau_"r" = "mg"."b"/2` ....(3)
The car does not topple as long as the restoring torque `tau_"r"` counterbalances the toppling torque `tau_"r"`.
Thus, to avoid the risk of rollover, the maximum speed that the car can have is given by
`("mv"^2/"r")"h" = "mg"."b"/2`
`therefore "v"_"max" = sqrt("rbg"/"2h")` ...(4)
Thus, vehicle tends to roll when the radial acceleration reaches a point where inner wheels of the four-wheeler are lifted off of the ground and the vehicle is rotated outward. A rollover occurs when the gravitational force `vec"mg"` passes through the pivot point of the outer wheels, i.e., the C.G. is above the line of contact of the outer wheels. Equation (3) shows that this maximum speed is high for a car with larger track width and lower center of gravity.
APPEARS IN
संबंधित प्रश्न
A thin walled hollow cylinder is rolling down an incline, without slipping. At any instant, without slipping. At any instant, the ratio "Rotational K.E.: Translational K.E.: Total K.E." is ______.
Answer in brief:
Why are curved roads banked?
Do we need a banked road for a two-wheeler? Explain.
The coefficient of static friction between a coin and a gramophone disc is 0.5. Radius of the disc is 8 cm. Initially the center of the coin is 2 cm away from the center of the disc. At what minimum frequency will it start slipping from there? By what factor will the answer change if the coin is almost at the rim? (use g = π2m/s2)
Answer in Brief:
A flywheel used to prepare earthenware pots is set into rotation at 100 rpm. It is in the form of a disc of mass 10 kg and a radius 0.4 m. A lump of clay (to be taken equivalent to a particle) of mass 1.6 kg falls on it and adheres to it at a certain distance x from the center. Calculate x if the wheel now rotates at 80 rpm.
Starting from rest, an object rolls down along an incline that rises by 3 in every 5 (along with it). The object gains a speed of `sqrt10` m/s as it travels a distance of `5/3` m along the incline. What can be the possible shape/s of the object?
A big dumb-bell is prepared by using a uniform rod of mass 60 g and length 20 cm. Two identical solid spheres of mass 25 g and radius 10 cm each are at the two ends of the rod. Calculate the moment of inertia of the dumb-bell when rotated about an axis passing through its centre and perpendicular to the length.
Does the angle of banking depend on the mass of the vehicle?
A hollow sphere has a radius of 6.4 m. what is the minimum velocity required by a motorcyclist at the bottom to complete the circle.
A bend in a level road has a radius of 100m. find the maximum speed which a car turning this bend may have without skidding if the coefficient of friction between the tires and road is 0.8.
Derive an expression for maximum safety speed with which a vehicle should move along a curved horizontal road. State the significance of it.
A bucket containing water is tied to one end of a rope 5 m long and it is rotated in a vertical circle about the other end. Find the number of rotations per minute in order that the water in the bucket may not spill.
A railway track goes around a curve having a radius of curvature of 1 km. The distance between the rails is 1 m. Find the elevation of the outer rail above the inner rail so that there is no side pressure against the rails when a train goes around the curve at 36 km/hr.
Obtain an expression for maximum safety speed with which a vehicle can be safely driven along a curved banked road.
A particle undergoes uniform circular motion. The angular momentum of the particle remains conserved about, ______
When a mass is rotating in a plane about a fixed point, its angular momentum is directed along, ______
Give any two examples of torque in day-to-day life.
What is the relation between torque and angular momentum?
Discuss conservation of angular momentum with example.
A flywheel rotates with uniform angular acceleration. If its angular velocity increases from `20pi` rad/s to `40pi` rad/s in 10 seconds. Find the number of rotations in that period.
A uniform metallic rod rotates about its perpendicular bisector with constant angular speed. If it is heated uniformly to raise its temperature to a certain value, its speed of rotation ______.
What is the difference between rotation and revolution?
