Advertisements
Advertisements
प्रश्न
Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate.)
Advertisements
उत्तर
Axiom 5 states that the whole is greater than the part. This axiom is known as a universal truth because it holds true in any field and not just in the field of mathematics. Let us take two cases − one in the field of mathematics and one other than that.
Case I
Let t represent a whole quantity, and only a, b, and c are parts of it.
t = a + b + c
Clearly, t will be greater than all its parts a, b, and c.
Therefore, it is rightly said that the whole is greater than the part.
Case II
Let us consider the continent Asia. Then, let us consider a country India which belongs to Asia. India is a part of Asia and it can also be observed that Asia is greater than India. That is why we can say that the whole is greater than the part. This is true for anything in any part of the world and is thus a universal truth.
APPEARS IN
संबंधित प्रश्न
How many least number of distinct points determine a unique plane?
The total number of propositions in the Elements are ______.
Boundaries of solids are ______.
In Indus Valley Civilisation (about 3000 B.C.), the bricks used for construction work were having dimensions in the ratio ______.
Pythagoras was a student of ______.
The boundaries of the solids are curves.
The statements that are proved are called axioms.
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have AB = BC, BX = BY. Show that AX = CY.
Solve the following question using appropriate Euclid’s axiom:
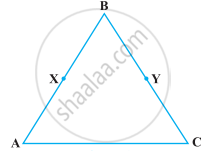
In the following figure, we have BX = `1/2` AB, BY = `1/2` BC and AB = BC. Show that BX = BY.
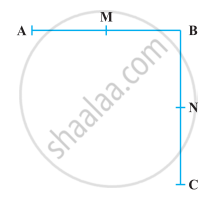
In the following figure BM = BN, M is the mid-point of AB and N is the mid-point of BC. Show that AB = BC.
