Advertisements
Advertisements
प्रश्न
Write one balanced equation to show Nuclear fission
Write any one balanced equation representing nuclear fission
उत्तर १
Nuclear Fission :
When a slow neutron strikes `""_92U^235` nucleus, it is absorbed by the nucleus and an isotope `U^236` is formed. But `U^236`, is highly unstable, is immediately broken into two fragments and emits neutrons and energy. This fission can be represented by the following equation
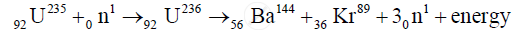
उत्तर २
Nuclear fission:
`""_0^1n + ""_92^235U -> ""_56^144Ba + ""_36^89Kr + 3 ""_0^1n`
APPEARS IN
संबंधित प्रश्न
Distinguish between nuclear fission and fusion. Show how in both these processes energy is released. Calculate the energy release in MeV in the deuterium-tritium fusion reaction :
`""_1^2H+_1^3H->_2^4He+n`
Using the data :
m(`""_1^2H`) = 2.014102 u
m(`""_1^3H`) = 3.016049 u
m(`""_2^4He`) = 4.002603 u
mn = 1.008665 u
1u = 931.5 MeV/c2
During a nuclear fission reaction,
Show that the minimum energy needed to separate a proton from a nucleus with Zprotons and N neutrons is `ΔE = (M_(Z-1,N) + M_B - M_(Z,N))c^2`
where MZ,N = mass of an atom with Z protons and N neutrons in the nucleus and MB = mass of a hydrogen atom. This energy is known as proton-separation energy.
Calculate the Q-values of the following fusion reactions :-
(a) `""_1^2H + ""_1^2H → ""_1^3H + ""_1^1H`
(b) `""_1^2H + ""_1^2H → ""_2^3H + n`
(c) `""_1^2H + ""_1^3H → _2^4H + n`.
Atomic masses are `m(""_1^2H) = 2.014102 "u", m(""_1^3H) = 3.016049 "u", m(""_2^3He) = 3.016029 "u", m(""_2^4He) = 4.002603 "u".`
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
Write one balanced reaction representing nuclear fusion.
In our Nature, where is the nuclear fusion reaction taking place continuously?
Explain in detail the four fundamental forces in nature.
Briefly explain the elementary particles present in nature.
A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the lower surface to steam at 100°C. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of the slab is:
(Given latent heat of fusion of ice = 3.36 × 105 J kg−1)
The curve of binding energy per nucleon as a function of atomic mass number has a sharp peak for helium nucleus. This implies that helium nucleus is ______.
