Advertisements
Advertisements
Question
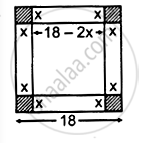
18 सेमी भुजा के टिन के किसी वर्गाकार टुकड़े से प्रत्येक कोने पर एक वर्ग काटकर तथा इस प्रकार बने टिन के फलकों को मोड़कर ढक्कन रहित एक संदूक बनाना है। काटे जाने वाले वर्ग की भुजा कितनी होगी जिससे संदूक का आयतन उच्चतम होगा?
Solution 1
माना वर्ग की प्रत्येक भुजा x सेमी काटी गई है।
∴ संदूक के लिए,
लंबाई = 18 - 2x
चौड़ाई = 18 - 2x
ऊँचाई = x
आयतन V = लंबाई × चौड़ाई × ऊँचाई
= x(18 - 2x) (18 - 2x)
= x(18 – 2x)x2 …(1)
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,
`"dV"/"dx"` = x. 2 (18 - 2x) (-2) = (18 - 2x)2. 1
= (18 - 2x) (- 4x + 18 - 2x) = (18 - 2x) (18 - 6x) ...(2)
उच्चतम व निम्नतम मान के लिए, `"dV"/"dx" = 0`
⇒ (18 - 2x)(18 - 6x) = 0
⇒ 18 - 2x = 0
⇒ 2x = 18
⇒ x = 9
तथा 18 - 6x = 0
⇒ x `= 18/6 = 3`
`therefore` x = 3, 9
परंतु x = 9 सेमी संभव नहीं है।
समीकरण (2) का पुन: के सापेक्ष अवकलन करने पर,
`("d"^2"V")/"dx"^2` = (18 - 2x) (- 6) + (18 - 6x) (- 2)
x = 3 पर, `("d"^2"V")/"dx"^2` = (18 - 2 × 3) (- 6) + (18 - 6 × 3) (- 2)
= (18 - 6) (- 6) + (18 - 18) (-2)
= 12 × (-6) + 0
= - 72 < 0, - ve
`therefore` x = 3 पर आयतन अधिकतम होगा अर्थात वर्ग की भुजा प्रत्येक कोने से 3 सेमी काटी गई है तो आयतन उच्चतम होगा।
Solution 2
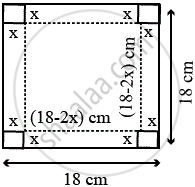
मान लीजिए x सेमी उस वर्ग की प्रत्येक भुजा की लंबाई है जिसे 18 सेमी भुजा वाली वर्गाकार टिन शीट के प्रत्येक कोने से काटा जाना है।
मान लीजिए V फ्लैप को मोड़ने से बने खुले संदूक का आयतन है, तो,
V = x (18 - 2x) (18 - 2x) = 4x (9 - x)2
= 4 (x3 - 18x2 + 81x)
x के संबंध में विभेद करने पर, हमें प्राप्त होता है
`(dV)/dx = 4(3x^2 - 36x + 81) = 12 (x^2 - 12x + 27)`
अधिकतम/न्यूनतम मात्रा के लिए
`(dV)/dx = 0`
⇒ 12 (x2 - 12x + 27) = 0
⇒ 12 (x - 3) (x - 9) = 0
⇒ x = 3, 9 परंतु 0 < x < 9
⇒ x = 3
`((d^2V)/dx^2) = 12 (2x - 12) = 24 (x - 6)`
और `((d^2V)/dx^2)_(x=3) = 24 (3 - 6) = -72 <0`
⇒ V का मान x = 3 पर अधिकतम है
अतः, जब काटे जाने वाले वर्ग की भुजा 3 सेमी हो, तो संदूक का आयतन अधिकतम होगा।
APPEARS IN
RELATED QUESTIONS
`y = [x (x - 1) + 1]^(1/3), 0 le x le 1,` का उच्चतम मान है:
निम्नलिखित दिए गए फलन के उच्चतम या निम्नतम मान, यदि कोई हो तो ज्ञात कीजिए:
f(x) = 9x2 + 12x + 2
निम्नलिखित दिए गए फलन के उच्चतम या निम्नतम मान, यदि कोई हो तो ज्ञात कीजिए:
g(x) = x3 + 1
निम्नलिखित दिए गए फलन के उच्चतम मान या निम्नतम मान, यदि कोई हो तो, ज्ञात कीजिए:
f(x) = |x + 2| - 1
निम्नलिखित दिए गए फलन के उच्चतम मान या निम्नतम मान, यदि कोई हो तो, ज्ञात कीजिए:
f(x) = |sin 4x + 3|
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
`h(x) = sin x + cos x, 0 < x < pi/2`
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
f(x) = x3 - 6x2 + 9x + 15
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
g(x) = `x/2 + 2/x, x > 0`
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
f(x) `= x sqrt(1 - x), 0 < x < 1`
सिद्ध कीजिए कि निम्नलिखित फलन को उच्चतम या निम्नतम मान नहीं है:
h(x) = x3 + x2 + x + 1
प्रदत्त अंतराल में निम्नलिखित फलन के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए।
f(x) = x3, x ∈ [-2, 2]
प्रदत्त अंतराल में निम्नलिखित फलन के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए।
f(x) = sin x + cos x, x `in [0, pi]`
प्रदत्त अंतराल में निम्नलिखित फलन के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए।
f(x) = (x - 1)2 + 3, x `in` [-3, 1]
फलन sin x + cos x का उच्चतम मान क्या है?
वक्र x2 = 2y पर (0, 5) से न्यूनतम दूरी पर स्थित बिंदु है:
ऐसी दो संख्याएँ ज्ञात कीजिए जिनका योग 24 है और जिनका गुणनफल उच्चतम हो।
ऐसी दो धन संख्याएँ x और y ज्ञात कीजिए ताकि x + y = 60 और xy3 उच्चतम हो।
45 cm × 24 cm की टिन की आयताकार चादर के चारों कोनों से समान भुजा का एक वर्गाकार निकालने के पश्चात् खुला हुआ एक संदूक बनाया जाता है। वर्गों की भुजा की माप ज्ञात कीजिये जिसके काटने पर बने संदूक का आयतन महत्तम होगा।
सिद्ध कीजिए कि एक दिए वृत्त के अंर्तगत सभी आयतों में वर्ग का क्षेत्रफल उच्चतम होता है।
सिद्ध कीजिए कि प्रदत्त पृष्ठ एवं महत्तम आयतन के बेलन की ऊँचाई आधार के व्यास के बराबर होती है।
एक 28 cm लंबे तार को दो टुकड़ों में विभक्त किया जाना है। एक टुकड़े से वर्ग तथा दूसरे से वृत्त बनाया जाना है। दोनों टुकड़ों की लंबाई कितनी होनी चाहिए जिससे वर्ग एवं वृत्त का सम्मिलित क्षेत्रफल न्यूनतम हो?
सिद्ध कीजिए कि न्यूनतम पृष्ठ पर दिए आयतन के लंब वृत्तीय शंकु की ऊँचाई, आधार की त्रिज्या की `sqrt2` गुनी होती है।
सिद्ध कीजिए कि R त्रिज्या के गोले के अन्तर्गत विशालतम शंकु का आयतन गोले के आयतन का `8/27` होता है।
सिद्ध कीजिए कि अर्द्धशीर्ष कोण और ऊँचाई h के लम्ब वृत्तीय शंकु के अन्तर्गत अधिकतम आयतन के बेलन की ऊँचाई शंकु के ऊँचाई की एक-तिहाई है और बेलन का अधिकतम आयतन `4/27` = πh3 tan2 α है।
वक्र x = t2 + 3t – 8, y = 2t2 – 2t -5 के बिन्दु (2, -1) पर स्पर्श रेखा की प्रवणता है-
