Advertisements
Advertisements
Question
70 पैकेटों में चाय के भार नीचे दी सारणी में दर्शाए गये हैं:
| भार (ग्राम में) | पैकेटों की संख्या |
| 200 – 201 | 13 |
| 201 – 202 | 27 |
| 202 – 203 | 18 |
| 203 – 204 | 10 |
| 204 – 205 | 1 |
| 205 – 206 | 1 |
इन आँकड़ों के लिए, 'से कम प्रकार' का तोरण खींचिए तथा इसका प्रयोग माध्यक भार ज्ञात करने में कीजए।
Solution
हम देखते हैं कि, 200 से कम पैकेटों की संख्या 0 है।
इसी प्रकार, 201 से कम में 0 – 200 तक पैकेटों की संख्या के साथ-साथ 200 – 201 तक पैकेटों की संख्या भी शामिल है।
तो, 201 से कम पैकेटों की कुल संख्या 0 + 13 = 13 है।
हम कहते हैं कि, वर्ग 200 – 201 की संचयी आवृत्ति 13 है।
इसी प्रकार अन्य वर्ग के लिए भी।
|
से कम प्रकार |
|
|
भार (ग्राम में) |
पैकेटों की संख्या |
|
200 से कम |
0 |
|
201 से कम |
0 + 13 = 13 |
|
202 से कम |
27 + 13 = 40 |
|
203 से कम |
18 + 40 = 58 |
|
204 से कम |
10 + 58 = 68 |
|
205 से कम |
1 + 68 = 69 |
|
206 से कम |
1 + 69 = 70 |
से कम प्रकार का तोरण निकालने के लिए, हम बिंदुओं को आलेखित करते हैं (200, 0), (201, 13), (202, 40) (203, 58), (204, 68), (205, 69) और (206, 70) कागज पर और मुक्त हाथ से जुड़ें।
∴ पैकेटों की कुल संख्या (n) = 70
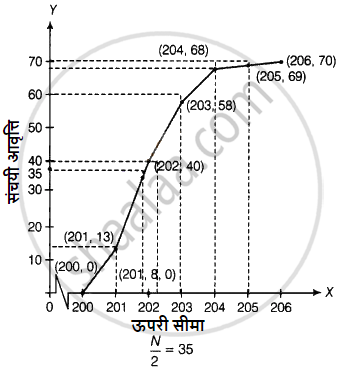
सबसे पहले, हम Y-अक्ष पर एक बिंदु (0, 35) आलेखित करते हैं और X-अक्ष के समानांतर एक रेखा y = 35 खींचते हैं।
रेखा तोरण से कम वक्र को एक बिंदु पर काटती है।
हम उस बिंदु पर एक रेखा खींचते हैं जो X-अक्ष पर लंबवत है।
X-अक्ष पर लंबवत रेखा का पाद आवश्यक माध्यिका है।
∴ माध्यिका भार = 201.8 ग्राम
APPEARS IN
RELATED QUESTIONS
निम्नलिखित सरणी किसी मोहल्ले के 25 परिवारों में भोजन पर हुए दैनिक व्यय को दर्शाती है:
| दैनिक व्यय (रुपये में) | 100 − 150 | 150 − 200 | 200 − 250 | 250 − 300 | 300 − 350 |
| परिवारों की संख्या | 4 | 5 | 12 | 2 | 2 |
एक उपयुक्त विधि द्वारा भोजन पर हुआ माध्य व्यय ज्ञात कीजिए।
यदि नीचे दिए हुए बंटन का माध्यक 28.5 हो तो x और y के मान ज्ञात कीजिए:
| कक्षा अन्तराल | आवृत्ति |
| 0 - 10 | 5 |
| 10 - 20 | x |
| 20 - 30 | 20 |
| 30 - 40 | 15 |
| 40 - 50 | y |
| 50 - 60 | 5 |
| Total | 60 |
एक पौधे की 40 पत्तियों की लंबाइयाँ निकटतम मिलीमिटरों में मापी जाती है तथा प्राप्त आँकड़ों को निम्नलिखित सारणी के रुप में निरुपित किया जाता है:
| लंबाई (mm में) | पत्तियों की संख्या |
| 118 − 126 | 3 |
| 127 − 135 | 5 |
| 136 − 144 | 9 |
| 145 − 153 | 12 |
| 154 − 162 | 5 |
| 163 − 171 | 4 |
| 172 − 180 | 2 |
पत्तियों की माध्यक लंबाई ज्ञात कीजिए।
संकेत: माध्यक ज्ञात करने के लिए, आँकड़ो को सतत वर्ग अंतरालों में बदलना पड़ेगा, क्योकिं सूत्र में वर्ग 117.5 - 126.5 , 126.5 - 135.5 ,…,171.5 - 180.5 अंतरालों को सतत माना गया है। तब ये वर्ग में बदल जाते है।
निम्नलिखित सारणी 400 नियाॅन लैंपों के जीवन कालों को प्रदर्शित करती है:
| जीवन काल (घंटों में) | लैंप की संख्या |
| 1500 – 2000 | 14 |
| 2000 – 2500 | 56 |
| 2500 – 3000 | 60 |
| 3000 – 3500 | 86 |
| 3500 – 4000 | 74 |
| 4000 – 4500 | 62 |
| 4500 – 5000 | 48 |
एक लैंप का माध्यक जीवन काल ज्ञात कीजिए।
नीचे दिया हुआ बंटन एक कक्षा के 30 विद्यार्थियों के भार दर्शा रहा है। विद्यार्थियों का माध्यक भार ज्ञात कीजिए।
| वजन (किलो में) | 40−45 | 45−50 | 50−55 | 55−60 | 60−65 | 65−70 | 70−75 |
| छात्रों की संख्या | 2 | 3 | 8 | 6 | 6 | 3 | 2 |
600 परिवारों की साप्ताहिक आय नीचे सारणीबद्ध है:
| साप्ताहिक आय (रू में) |
परिवारों की संख्या |
| 0 – 1000 | 250 |
| 1000 – 2000 | 190 |
| 2000 – 3000 | 100 |
| 3000 – 4000 | 40 |
| 4000 – 5000 | 15 |
| 5000 – 6000 | 5 |
| कुल | 600 |
माध्यम आय अभिकलित कीजिए।
किसी क्रिकेट कोचिंग केंद्र पर 33 खिलाडियों की गेंदबाजी करने की अधिकतम चालें (km प्रति घंटा में) इस प्रकार है:
|
चाल (km/h) |
85 – 100 |
100 – 115 |
115 – 130 |
130 – 145 |
|
खिलाड़ियों की संख्या |
11 | 9 | 8 | 5 |
गेंदबाजी की माध्यक चाल परिकलित कीजिए।
70 पैकेटों में चाय के भार नीचे दी सारणी में दर्शाए गये हैं:
| भार (ग्राम में) | पैकेटों की संख्या |
| 200 – 201 | 13 |
| 201 – 202 | 27 |
| 202 – 203 | 18 |
| 203 – 204 | 10 |
| 204 – 205 | 1 |
| 205 – 206 | 1 |
इन आँकड़ों के लिए, 'से कम प्रकार' और 'से अधिक प्रकार' के तोरण खींचिए तथा इनका माध्यक भार ज्ञात करने में प्रयोग कीजिए।
96 बच्चों की लंबाइयों (ऊँचाइयों) (cm में) का बंटन नीचे दिया गया है:
|
लंबाई (cm में) |
बच्चों की संख्या |
| 124 – 128 | 5 |
| 128 – 132 | 8 |
| 132 – 136 | 17 |
| 136 – 140 | 24 |
| 140 – 144 | 16 |
| 144 – 148 | 12 |
| 148 – 152 | 6 |
| 152 – 156 | 4 |
| 156 – 160 | 3 |
| 160 – 164 | 1 |
इन आँकड़ों के लिए, 'से कम प्रकार' की संचयी बारंबारता वक्र खींचिए और इसका बच्चों की माध्यक लंबाई ज्ञात करने में प्रयोग कीजिए।
किसी मोबाइल फोन पर किये गये कॉलों के समय-काल का बारंबारता बंटन नीचे दिया गया है:
|
समय काल (सेकंडों में) |
कॉलों की संख्या |
| 95 – 125 | 14 |
| 125 – 155 | 22 |
| 155 – 185 | 28 |
| 185 – 215 | 21 |
| 215 – 245 | 15 |
इन कॉलों का औसत समय काल (सेकंडों में) परिकलित कीजिए तथा साथ ही संचयी बारंबारता वक्र से माध्यक भी ज्ञात कीजिए।
