Advertisements
Advertisements
Question
A(20, 10), B(0, 20) को जोड़ने वाले रेखाखंड AB को पांच सर्वांगसम रेखाखंडों में विभाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।
Solution
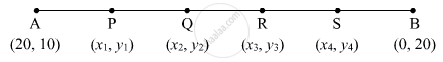
A(20, 10) और B(0, 20).
मानो कि, P(x1, y1); Q(x2, y2); R(x3, y3) और S(x4, y4) यह रेख AB को पाँच सर्वांगसम रेखाखंडों में विभाजित करता है |
∴ AP = PQ = QR = RS = SB ............(1)
`"AP"/"BP" = "AP"/("PQ + QR + RS + SB")` ................(P-Q-R, Q-R-S और R-S-B)
∴ `"AP"/"PB" = "AP"/("AP + AP + AP + AP")` ........[(1) से]
∴ `"AP"/"PB" = "AP"/"4AP"`
∴ `"AP"/"PB" = 1/4`
∴ AP : PB = 1 : 4
∴ बिंदु P, रेख AB को 1 : 4 के अनुपात में विभाजित करता है |
विभाजन के सूत्र से,
`x_1 = (1(0) + 4(20))/(1 + 4)`
∴ `x_1 = 80/5`
∴ `x_1 = 16`
∴ `y_1 = (1(20) + 4(10))/(1 + 4)`
∴ `y_1 = 60/5`
∴ `y_1 = 12`
∴ बिंदु P का निर्देशांक (16, 12) है |
बिंदु P, रेख AQ का मध्यबिंदु है |
∴ मध्यबिंदु के सूत्र से,
16 = `(20 + x_2)/2`
∴ 32 = 20 + x2
∴ `x_2 = 32 - 20`
∴ `x_2 = 12`
12 = `(10 + y_2)/2`
∴ 24 = 10 + `y_2`
∴ `y_2 = 24 - 10`
∴ `y_2 = 14`
बिंदु Q का निर्देशांक (12, 14) है |
बिंदु R, रेख PB का मध्यबिंदु है |
∴ मध्यबिंदु के सूत्र से,
`x_3 = (16 + 0)/2`
∴ `x_3 = 16/2`
∴ `x_3 = 8`
∴ `y_3 = (12 + 20)/2`
∴ `y_3 = 32/2`
∴ `y_3 = 16`
∴ बिंदु R का निर्देशांक (8, 16) है |
बिंदु S, रेख RB का मध्यबिंदु है |
∴ मध्यबिंदु के सूत्र से,
`x_4 = (8 + 0)/2`
∴ `x_4 = 8/2`
∴ `x_4 = 4`
∴ `y_4 = (16 + 20)/2`
∴ `y_4 = 36/2`
∴ `y_4 = 18`
∴ बिंदु S का निर्देशांक (4, 18) है |
∴ रेखाखंड AB को पाँच सर्वांगसम रेखाखंडों में विभाजित करने वाले बिंदुओं के निर्देशांक (16, 12); (12, 14); (8, 16) और (4, 18) हैं |
APPEARS IN
RELATED QUESTIONS
नीचे दिए गए उदाहरण में रेखाखंड PQ को a : b के अनुपात में विभाजित करने वाले बिंदु A के निर्देशांक ज्ञात कीजिए।
P(-3, 7), Q(1, -4), a : b = 2 : 1
नीचे दिए गए उदाहरण में रेखाखंड PQ को a : b के अनुपात में विभाजित करने वाले बिंदु A के निर्देशांक ज्ञात कीजिए।
P(2, 6), Q(-4, 1), a : b = 1 : 2
A(-14, -10), B(6, -2) को जोड़ने वाले रेखाखंड AB को चार सर्वांगसम रेखाखंडों में विभाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।
विभाजन सूत्र का प्रयोग करके दिखाइए कि बिंदु
A(2, –3, 4), B(−1, 2, 1) तथा C`(0, 1/3, 2)` संरेख हैं।
बिंदुओं (-3, 10) और (6, -8) को जोड़ने वाले रेखाखंड को बिंदु (-1, 6) किस अनुपात में विभाजित करता है?
उस बिंदु के निर्देशांक ज्ञात कीजिए, जो बिंदुओं (-1, 7) और (4, -3) को मिलाने वाले रेखाखंड को 2 : 3 के अनुपात में विभाजित करता है।
बिंदुओं A(2, -2) और B(3, 7) को जोड़ने वाले रेखाखंड को रेखा 2x + y - 4 = 0 जिस अनुपात में विभाजित करती है उसे ज्ञात कीजिए।
ज्ञात कीजिए कि बिंदु `P(3/4, 5/12)`, बिंदुओं `A(1/2, 3/2)` और B(2, –5) को मिलाने वाले रेखाखंड को किस अनुपात में विभाजित करता हैं।
वह अनुपात ज्ञात कीजिए, जिसमें रेखा 2x + 3y – 5 = 0, बिंदुओं (8, –9) और (2, 1) को मिलाने वाले रेखाखंड को विभाजित करती है। विभाजन बिंदु के निर्देशांक भी ज्ञात कीजिए।
यदि बिंदुओं A(1, –2), B(2, 3), C(a, 2) और D(– 4, –3) से एक समांतर चतुर्भुज बनता है, तो a का मान ज्ञात कीजिए तथा AB को आधार लेकर उसकी संगत ऊँचाई ज्ञात कीजिए।
