Advertisements
Advertisements
Question
यदि बिंदुओं A(1, –2), B(2, 3), C(a, 2) और D(– 4, –3) से एक समांतर चतुर्भुज बनता है, तो a का मान ज्ञात कीजिए तथा AB को आधार लेकर उसकी संगत ऊँचाई ज्ञात कीजिए।
Solution
हम जानते हैं कि समांतर चतुर्भुज में विकर्ण एक दूसरे को समद्विभाजित करते हैं।
अर्थात, AC का मध्य-बिंदु = BD का मध्य-बिंदु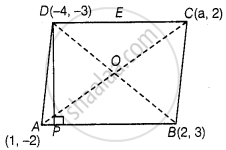
⇒ `((1 + a)/2, (-2 + 2)/2) = ((2 - 4)/2, (3 - 3)/2)` ...`["चूंकि, बिंदु वाले रेखाखंड का मध्य-बिंदु" (x_1, y_1) "और" (x_2, y_2) "is" ((x_1 + x_2)/2, (y_1 + y_2)/2)]`
⇒ `(1 + a)/2 = (2 - 4)/2 = (-2)/2` = – 1
⇒ 1 + a = – 2
⇒ a = – 3
तो, a का अभीष्ट मान – 3 है।
दिया गया है कि, AB को एक समांतर चतुर्भुज का आधार माना गया है और D से AB तक एक लंब खींचा गया है जो AB को P पर मिलता है।
तो, DP एक समांतर चतुर्भुज की ऊँचाई है।
अब, बिंदु (1, – 2) और (2, 3) से गुजरने वाले आधार AB का समीकरण है।
⇒ (y – y1) = `(y_2 - y_1)/(x_2 - x_1)(x - x_1)`
⇒ (y + 2) = `(3 + 2)/(2 - 1) (x - 1)`
⇒ (y + 2) = 5(x – 1)
⇒ 5x – y = 7 ...(i)
AB की ढलान, मान लीजिए, m1 = `(y_2 - y_1)/(x_2 - x_1) = (3 + 2)/(2 - 1)` = 5
माना DP का ढलान m2 है।
चूँकि, DP, AB के लंबवत है।
लंबवतता की स्थिति से,
m1 · m2 = – 1
⇒ 5 · m2 = – 1
⇒ m2 = `-1/5`
अब, DP का समीकरण, जिसका ढलान `(-1/5)` है और बिंदु (– 4, – 3) से गुजर रहा है।
(y – y1) = m2(x – x1)
⇒ (y + 3) = `-1/5(x + 4)`
⇒ 5y + 15 = – x – 4
⇒ x + 5y = – 19 ...(ii)
समीकरण (i) और (ii) को जोड़ने पर, हमें प्रतिच्छेदन बिंदु P प्राप्त होता है।
समीकरण (i) से y का मान समीकरण (ii) में रखने पर, हमें प्राप्त होता है।
x + 5(5x – 7) = – 19 ...[समीकरण (i) का प्रयोग करके]
⇒ x + 25x – 35 = – 19
⇒ 26x = 16
∴ x = `8/13`
x का मान समीकरण (i) में रखने पर, हमें प्राप्त होता है।
y = `5(8/13) - 7 = 40/13 - 7`
⇒ y = `(40 - 91)/13`
⇒ y = `(-51)/13`
∴ बिंदु P के निर्देशांक ≡ `(8/13, (-51)/13)`
तो, समांतर चतुर्भुज की ऊंचाई की लंबाई,
DP = `sqrt((8/13 + 4)^2 + ((-51)/13 + 3)^2` ...`[∵ "दूरी सूत्र द्वारा, दो बिंदुओं के बीच की दूरी" (x_1, y_1) "and" (x_2, y_2) "is" d = sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)]`
⇒ DP = `sqrt((60/13)^2 + ((-12)/13)^2`
= `1/13 sqrt(3600 + 144)`
= `1/13 sqrt(3744)`
= `(12sqrt(26))/13`
अतः, एक समांतर चतुर्भुज की ऊंचाई की आवश्यक लंबाई `(12sqrt(26))/13` है।
APPEARS IN
RELATED QUESTIONS
नीचे दिए गए उदाहरण में रेखाखंड PQ को a : b के अनुपात में विभाजित करने वाले बिंदु A के निर्देशांक ज्ञात कीजिए।
P(-2, -5), Q(4, 3), a : b = 3 : 4
यदि P-T-Q है, तो बिंदु T(-1, 6), बिंदु P(-3, 10) और बिंदु Q(6, -8) को जोड़ने वाले रेखाखंड को किस अनुपात में विभाजित करता है, ज्ञात कीजिए।
A(-14, -10), B(6, -2) को जोड़ने वाले रेखाखंड AB को चार सर्वांगसम रेखाखंडों में विभाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।
A(20, 10), B(0, 20) को जोड़ने वाले रेखाखंड AB को पांच सर्वांगसम रेखाखंडों में विभाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।
A(3, 8) और B(-9, 3) इन बिंदुओं को जोड़ने वाले रेखाखंड को Y- अक्ष किस अनुपात में विभाजित करता है।
P(4, 2, –6) और Q(10, –16, 6) के मिलाने वाली रेखा खंड PQ को सम त्रि-भाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।
यदि A और B क्रमशः (-2, -2) और (2, -4) हो तो बिंदु P के निर्देशांक ज्ञात कीजिए ताकि AP = `3/7` AB हो और P रेखाखंड AB पर स्थित हो।
बिंदुओं (-3, 10) और (6, -8) को जोड़ने वाले रेखाखंड को बिंदु (-1, 6) किस अनुपात में विभाजित करता है?
उस बिंदु के निर्देशांक ज्ञात कीजिए, जो बिंदुओं (-1, 7) और (4, -3) को मिलाने वाले रेखाखंड को 2 : 3 के अनुपात में विभाजित करता है।
यदि बिंदु A(4, –3) तथा B(8, 5) हो, तो रेखाखंड AB को 3 : 1 के अनुपात में विभाजित करने वाले बिंदु P का निर्देशांक ज्ञात करने के लिए निम्न कृति पूर्ण करो:
कृति: 
x = `(mx_2 + nx_1)/square`
∴ x = `(3 xx 8 + 1 xx 4)/(3 + 1)`
∴ x = `(square + 4)/4`
∴ x = `square`,
y = `square/(m + n)`
∴ y = `(3 xx 5 + 1 xx (-3))/(3 + 1)`
∴ y = `(square - 3)/4`
∴ y = `square`
