Advertisements
Advertisements
Question
A capacitor of capacitance C is connected to a battery of emf ε at t = 0 through a resistance R. Find the maximum rate at which energy is stored in the capacitor. When does the rate have this maximum value?
Solution
The rate of growth of charge for the capacitor,
\[q = \epsilon C \left(1 − e^\frac{- t}{RC}\right)\]
Let E be the energy stored inside the capacitor. Then,
\[E = \frac{q^2}{2C} = \frac{\epsilon^2 C^2}{2C} \left( 1 - e^{- \frac{t}{RC}} \right)^2 \]
\[ \Rightarrow E = \frac{\epsilon^2 C}{2} \left( 1 - e^{- \frac{t}{RC}} \right)^2\]
Let r be the rate of energy stored inside the capacitor. Then,
\[r = \frac{dE}{dt} = \frac{2 \epsilon^2 C}{2}\left( 1 - e^{- \frac{t}{RC}} \right)\left( - e^{- \frac{t}{RC}} \right)\left( - \frac{1}{RC} \right)\]
\[ \Rightarrow r = \frac{\epsilon^2}{R}\left( 1 - e^{- \frac{t}{RC}} \right)\left( e^{- \frac{t}{RC}} \right)\]
\[\frac{dr}{dt} = \frac{\epsilon^2}{R}\left[ \left( - e^{- \frac{t}{RC}} \right)\left( - \frac{1}{RC} \right)\left( e^{- \frac{t}{RC}} \right) + \left( 1 - e^{- \frac{t}{RC}} \right)\left( e^{- \frac{t}{RC}} \right)\left( - \frac{1}{RC} \right) \right]\]
For r to be maximum,
\[\frac{dr}{dt} = 0\]
\[\Rightarrow \frac{\epsilon^2}{R}\left[ \left( - e^{- \frac{t}{RC}} \right)\left( - \frac{1}{RC} \right)\left( e^{- \frac{t}{RC}} \right) + \left( 1 - e^{- \frac{t}{RC}} \right)\left( e^{- \frac{t}{RC}} \right)\left( - \frac{1}{RC} \right) \right] = 0\]
\[ \Rightarrow \left[ \frac{e^{- \frac{2t}{RC}}}{RC} + \frac{e^{- \frac{2t}{RC}}}{RC} - \frac{e^\frac{- t}{RC}}{RC} \right] = 0\]
\[ \Rightarrow 2 e^{- \frac{2t}{RC}} = e^{- \frac{t}{RC}} \]
\[ \Rightarrow e^{- \frac{t}{RC}} = \frac{1}{2}\]
\[ \Rightarrow - \frac{t}{RC} = - \ln2\]
\[ \Rightarrow t = RC\ln2\]
APPEARS IN
RELATED QUESTIONS
Obtain the expression for the energy stored per unit volume in a charged parallel plate capacitor.
A 600 pF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 600 pF capacitor. How much electrostatic energy is lost in the process?
Find the ratio of energy stored in the two configurations if they are both connected to the same source.
A capacitor of capacitance 500 μF is connected to a battery through a 10 kΩ resistor. The charge stored in the capacitor in the first 5 s is larger than the charge stored in the next.
(a) 5 s
(b) 50 s
(c) 500 s
(d) 500 s
A capacitor C1 of capacitance 1 μF and a capacitor C2 of capacitance 2 μF are separately charged by a common battery for a long time. The two capacitors are then separately discharged through equal resistors. Both the discharge circuits are connected at t = 0.
(a) The current in each of the two discharging circuits is zero at t = 0.
(b) The currents in the two discharging circuits at t = 0 are equal but not zero.
(c) The currents in the two discharging circuits at t = 0 are unequal.
(d) C1 loses 50% of its initial charge sooner than C2 loses 50% of its initial charge.
A capacitance C, a resistance R and an emf ε are connected in series at t = 0. What is the maximum value of (a) the potential difference across the resistor (b) the current in the circuit (c) the potential difference across the capacitor (d) the energy stored in the capacitor (e) the power delivered by the battery and (f) the power converted into heat?
A 20 μF capacitor is joined to a battery of emf 6.0 V through a resistance of 100 Ω. Find the charge on the capacitor 2.0 ms after the connections are made.
A capacitance C charged to a potential difference V is discharged by connecting its plates through a resistance R. Find the heat dissipated in one time constant after the connections are made. Do this by calculating ∫ i2R dt and also by finding the decrease in the energy stored in the capacitor.
A capacitor of capacitance C is given a charge Q. At t = 0, it is connected to an ideal battery of emf ε through a resistance R. Find the charge on the capacitor at time t.
A metal sphere of radius R is charged to a potential V.
- Find the electrostatic energy stored in the electric field within a concentric sphere of radius 2 R.
- Show that the electrostatic field energy stored outside the sphere of radius 2 R equals that stored within it.
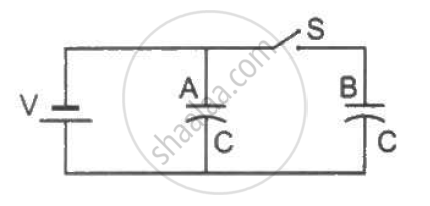
Figure shows two identical parallel plate capacitors connected to a battery through a switch S. Initially, the switch is closed so that the capacitors are completely charged. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant 3. Find the ratio of the initial total energy stored in the capacitors to the final total energy stored.
Choose the correct option:
Energy stored in a capacitor and dissipated during charging a capacitor bear a ratio.
A parallel plate condenser is immersed in an oil of dielectric constant 2. The field between the plates is ______.
A 2µF capacitor is charge to 100 volt and then its plate are connected by a conducting wire. The heat produced is:-
What fraction of the energy drawn from the charging battery is stored in a capacitor?
Prove that, if an insulated, uncharged conductor is placed near a charged conductor and no other conductors are present, the uncharged body must be intermediate in potential between that of the charged body and that of infinity.
A fully charged capacitor C with initial charge q0 is connected to a coil of self-inductance L at t = 0. The time at which the energy is stored equally between the electric and magnetic fields is ______.
A parallel plate capacitor (A) of capacitance C is charged by a battery to voltage V. The battery is disconnected and an uncharged capacitor (B) of capacitance 2C is connected across A. Find the ratio of total electrostatic energy stored in A and B finally and that stored in A initially.
In a capacitor of capacitance 20 µF, the distance between the plates is 2 mm. If a dielectric slab of width 1 mm and dielectric constant 2 is inserted between the plates, what is the new capacitance?
