Advertisements
Advertisements
Question
A charged particle is in motion having initial velocity `vecv` when it enters into a region of uniform magnetic field perpendicular to `vecv`. Because of the magnetic force the kinetic energy of the particle will ______.
Options
remain unchanged
get reduced
increase
be reduced to zero
Solution
A charged particle is in motion having initial velocity v when it enters into a region of uniform magnetic field perpendicular to v. Because of the magnetic force the kinetic energy of the particle will remain unchanged.
Explanation:
The work done by the magnetic force is always zero because the direction of motion due to the magnetic force is always perpendicular to it. When the particle enters the field the magnitude of the velocity stays the same while the direction changes and while the kinetic energy remains the same. It can only lead to a change in the direction of motion and not the speed. Hence there is going to be no change in the kinetic energy of the particle.
RELATED QUESTIONS
A rod of length l is moved horizontally with a uniform velocity 'v' in a direction perpendicular to its length through a region in which a uniform magnetic field is acting vertically downward. Derive the expression for the emf induced across the ends of the rod.
A circular coil carrying a current I has radius R and number of turns N. If all the three, i.e. the current
I, radius R and number of turns N are doubled, then, the magnetic field at its centre becomes:
(a) Double
(b) Half
(c) Four times
(d) One fourth
Explain the term hysteresis
Define magnetic lines of force
The free electrons in a conducting wire are in constant thermal motion. If such a wire, carrying no current, is placed in a magnetic field, is there a magnetic force on each free electron? Is there a magnetic force on the wire?
A straight horizontal wire of mass 10 mg and length 1.0 m carries a current of 2.0 A. What minimum magnetic field B should be applied in the region, so that the magnetic force on the wire may balance its weight?
Show that currents in two long, straight, parallel wires exert forces on each other. Derive the expression for the force per unit length on each conductor.
The magnetic moment is NOT associated with ____________.
A charged particle enters an environment of a strong and non-uniform magnetic field varying from point to point both in magnitude and direction, and comes out of it following a complicated trajectory. Would its final speed equal the initial speed if it suffered no collisions with the environment?
An electron travelling west to east enters a chamber having a uniform electrostatic field in north to south direction. Specify the direction in which a uniform magnetic field should be set up to prevent the electron from deflecting from its straight line path.
A magnetic field set up using Helmholtz coils is uniform in a small region and has a magnitude of 0.75 T. In the same region, a uniform electrostatic field is maintained in a direction normal to the common axis of the coils. A narrow beam of (single species) charged particles all accelerated through 15 kV enters this region in a direction perpendicular to both the axis of the coils and the electrostatic field. If the beam remains undeflected when the electrostatic field is 9.0 × 10–5 V m–1, make a simple guess as to what the beam contains. Why is the answer not unique?
Correct unit of magnetic field is ______.
- perpendicular to direction of velocity of charged particle.
-
perpendicular to direction of magnetic field.
-
parallel to direction of velocity of charged particle.
-
parallel to the direction of magnetic field.
The correct plot of the magnitude of magnetic field `vec"B"` vs distance r from centre of the wire is, if the radius of wire is R.
The phenomenon in which a magnetic field is produced in the space near a conductor carrying current is called ______
In the product `vec"F" = "q" (vec"υ" xx vec"B")`
= `"q" vec"υ" xx ("B"hat"i" +"B"hat"j" + "B"_0hat"k")`
For q = 1 and `vec"υ" = 2hat"i" + 4hat"j" + 6hat"k"` and
`vec"F" = 4hat"i" - 20hat"j" + 12hat"k"`
What will be the complete expression for `vec"B"`?
In the product
`overset(->)("F") = "q"(overset(->)(υ) xx overset(->)("B"))`
= `"q"overset(->)(υ) xx ("B"overset(^)("i") + "B" overset(^)("j") + "B"_0overset(^)("k"))`
For q = 1 and `overset(->)(υ) = 2overset(^)("i") + 4overset(^)("j") + 6overset(^)("k")` and
`overset(->)("F") = 4overset(^)("i") - 20overset(^)("j") + 12overset(^)("k")`
What will be the complete expression for `overset(->)("B")`?
The magnetic force depends on v which depends on the inertial frame of reference. Does then the magnetic force differ from inertial frame to frame? Is it reasonable that the net acceleration has a different value in different frames of reference?
A charged particle of charge e and mass m is moving in an electric field E and magnetic field B. Construct dimensionless quantities and quantities of dimension [T]–1.
A beam of light travelling along X-axis is described by the electric field Ey = 900 sin ω(t - x/c). The ratio of electric force to magnetic force on a charge q moving along Y-axis with a speed of 3 × 107 ms-1 will be : [Given speed of light = 3 × 108 ms-1]
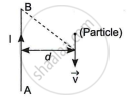
A long straight wire AB carries a current I. A particle (mass m and charge q) moves with a velocity `vec"v"`, parallel to the wire, at a distance d from it as shown in the figure. Obtain the expression for the force experienced by the particle and mention its directions.
A long straight conductor kept along X' X axis, carries a steady current I along the +x direction. At an instant t, a particle of mass m and charge q at point (x, y) moves with a velocity `vecv` along +y direction. Find the magnitude and direction of the force on the particle due to the conductor.
State dimensions of magnetic field.
What is the relation between Tesla and Gauss?
