Advertisements
Advertisements
Question
A cone and a hemisphere have the same base and the same height. Find the ratio between their volumes.
Solution
Let the radius of base be 'r' and the height be 'h'
Volume of cone, `V_c`
= `1/3pir^2h`
Volume of hemisphere, `V_h`
= `2/3pir^3`
`V_c/V_h = (1/3pir^2r)/(2/3pir^3)`
`=> V_c/V_h = 1/2`
APPEARS IN
RELATED QUESTIONS
The radius of a cone is 7 cm and area of curved surface is 176 `cm^2`. Find the slant height.
The height of a cone is 21 cm. Find the area of the base if the slant height is 28 cm.
There are two cones. The curved surface area of one is twice that of the other. The slant height of the later is twice that of the former. Find the ratio of their radii.
The diameter of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surface areas.
The volume of a conical tent is 1232 m3 and the area of the base floor is 154 m2. Calculate the:
- radius of the floor,
- height of the tent,
- length of the canvas required to cover this conical tent if its width is 2 m.
A solid metal sphere is cut through its center into 2 equal parts. If the diameter of the sphere is `3 1/2 cm`, find the total surface area of each part correct to two decimal places.
The radii of the internal and external surfaces of a metallic spherical shell are 3 cm and 5 cm respectively. It is melted and recast into a solid right circular cone of height 32 cm. Find the diameter of the base of the cone.
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed.
A buoy is made in the form of hemisphere surmounted by a right cone whose circular base coincides with the plane surface of hemisphere. The radius of the base of the cone is 3.5 metres and its volume is two-third of the hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two places of decimal.
A cubical block of side 7 cm is surmounted by a hemisphere of the largest size. Find the surface area of the resulting solid.
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm, are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
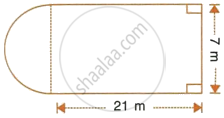
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.
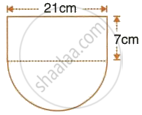
The given figure shows the cross section of a water channel consisting of a rectangle and a semi-circle. Assuming that the channel is always full, find the volume of water discharged through it in one minute if water is flowing at the rate of 20 cm per second. Give your answer in cubic metres correct to one place of decimal.
Find the radius of the circular base of the cone , if its volume is 154 cm3 and the perpendicular height is 12 cm
Find the curved surface area of a cone whose height is 8 cm and base diameter is 12 cm .
A buoy is made in the form of a hemisphere surmounted by a right circular cone whose circular base coincides with the plane surface of the hemisphere. The radius of the base of the cone is 3.5 m and its volume is two-third the volume of hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two decimal places.
The surface area of a solid sphere is increased by 21% without changing its shape. Find the percentage increase in its: volume
A right-angled triangle PQR where ∠Q = 90° is rotated about QR and PQ. If QR = 16 cm and PR = 20 cm, compare the curved surface areas of the right circular cones so formed by the triangle
The ratio of the radii of two right circular cones of the same height is 1 : 3. Find the ratio of their curved surface area when the height cone is 3 times the radius of the smaller cone.
